Техническое приложение I
Логарифмически-нормальные графики результатов измерения воздействий и средних воздействий
Ранее, в работах (I-1 ÷ I-6) обсуждалась полезность и удобность использования (миллиметровки с логарифмически-вероятностной шкалой) для построения графиков результатов измерений воздействий в промышленной гигиене. В этом приложении рассмотрена практическая сторона использования такой бумаги. Сначала описано, как её использовать. Затем приводится два примера - измерения воздействий, и средние результаты измерений на отдельных рабочих в группе.
На Фиг. I-1 и I-2 показаны образцы такой бумаги, смеющейся в продаже (2-цикловой и 3-цикловой). Обычно она охватывает тот диапазон значений, которые получаются при измерениях. Если требуются дополнительные циклы, отрезая и приклеивая соответственные участки, можно получить бумагу с 4 или 5 циклами.
При построении графиков первым шагом является ранжирование исходных данных, чтобы они располагались в порядке возрастания значений. Обычно наименьшим значением по оси ОХ является 1, а наибольшим - n, где n - число замеров, или число средних значений воздействия. Затем ранжированные значения наносят на график. Среди специалистов по статистике нет единого мнения о том, как правильно наносить результаты на такую бумагу. Широко используемый способ предложен в (I-7). Таблица I-1 взята из этой публикации. Она охватывает число значений n от 2 до 50, и также приводится уравнение для большего числа значений.
После построения результатов и получения субъективной оценки - что результаты укладываются на прямую линию - строится линейная регрессионная линия. Важно понимать, что при использовании логарифмически-нормальных шкал нельзя применять широко известный метод наименьших квадратов. Причины этого объясняются в (I-8).
Если (регрессионная) линия хорошо соответствует результатам измерений, то (специалист) не должен считать все результаты одинаково важными (ценными). На регрессионную линию в большей степени влияют результаты, которые находятся в центре (графика). Любые отклонения, которые наблюдаются в областях с большой и с маленькой вероятностями (например - <5% и >95%) на таком графике на такой бумаге будут преувеличены, излишне подчёркнуты. Особенно - при сравнении при той же абсолютной величине отличия в средней области (например - от 20 до 80%).
Например, при вероятности 99% отклонение в 15 раз больше, чем при вероятности 50%; а при вероятности 99.5% - в 28 раз. Из-за искажений, вносимых логарифмически-нормальной шкалой, невозможно даже приблизительно (определить) величину отклонений с помощью простой проверки. Схожие примеры искажений встречаются в картографии. При использовании проекции поверхности земного шара на плоскость Меркатера искажаются расстояния между точками, конкретно - в областях около полюсов расстояния между ними возрастают.
Такая бумага должна использоваться только для нанесения результатов, и для предварительной оценки того, соответствуют ли они логарифмически-нормальной модели (распределения результатов измерений). Она также полезна, когда нужно быстро сделать оценку среднего геометрического значения (GM) и стандартного геометрического отклонения (GSD) полученной логарифмически-нормальной модели. Но такую бумагу нельзя использовать для получения статистически-обоснованных оценок того, насколько хорошо регрессионная прямая линия соответствует результатам измерений. При ''подгонке'' прямой линии к точкам (результатам измерений) наблюдается следующее:
- Игнорируются все точки, которые находятся за пределами диапазона вероятностей 1 ÷ 99%.
- Из оставшихся предпочтение отдаётся тем, которые находятся ближе к центру (50%), то есть - в диапазоне 20 ÷ 80%.
Santner в (1-7) привёл указания (Фиг. I-3), которые помогают интерпретировать информацию на графике с логарифмически-нормальной системой координат. Также предлагались другие методы линеаризации результатов и способы построения графиков.
В (I-9) Hann and Shapiro приводят полезную информацию о построении графиков в логарифмически-нормальной системе координат. Там, в главе 8 ''Probability Plotting and Testing of Distributional Assumptions'' приводится много графиков вероятностных распределений.
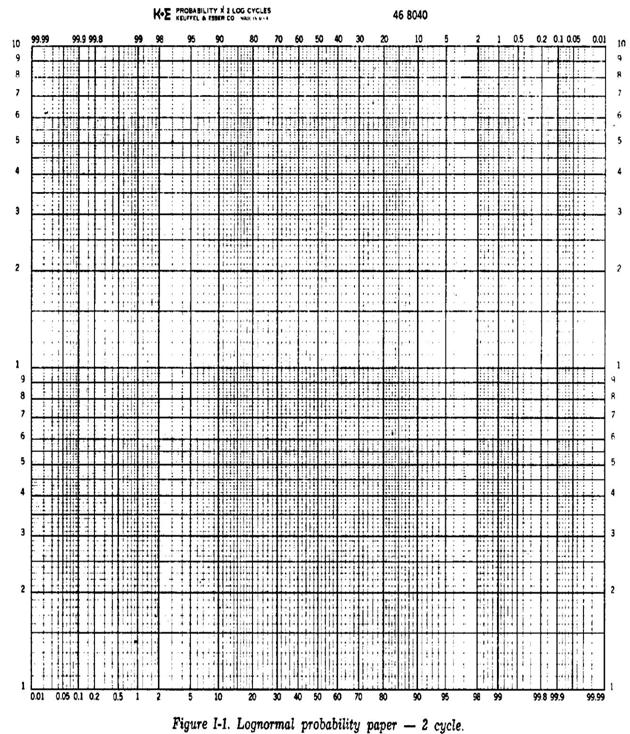
Фиг. I-1. Бумага с логарифмически-нормальными шкалами - двухцикловая
Там также приводятся графики, которые позволяют сравнить типичные отклонения от линейности (для графиков, построенных в логарифмически-нормальной системе координат) при использовании 20 и 50 значений (результатов измерений), взятых из разных распределений, у которых разные отклонения от нормального. При использовании (всего лишь) 20 значений, взятых из множества значений, соответствующих нормальному распределению, получаются значительные отклонения от нормального распределения (от линейности графика) из-за случайной изменчивости (взятых) значений.
В (I-10) Daniel and Wood тоже показали, какие бывают типичные отклонения от линейности из-за случайной изменчивости значений выборки. В их приложении 3А приводятся графики случайных нормальных отклонений при числе значений в выборке 8, 16, 32, 64 и 384. Они обнаружили, что при числе замеров 8 нельзя (даже) сделать выводы о том, нормально ли распределение вообще. При 16 значениях сохраняются значительные отклонения от линейности. При 32 и 64 значениях результат значительно улучшается, но продолжает не соответствовать прямой линии на ''концах'' распределения (вероятности менее 10% и более 90%).
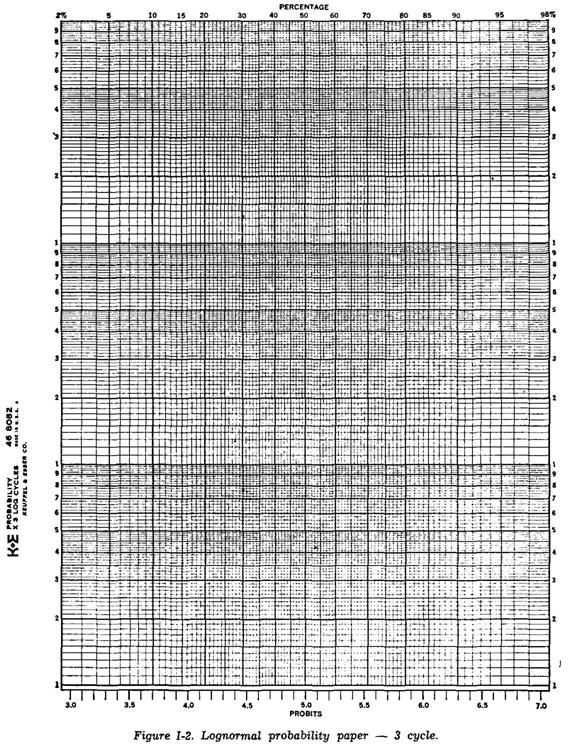
Фиг. I-2. Бумага с логарифмически-нормальными шкалами - трёхцикловая
После того, как была построена прямая линия, наилучшим образом соответствующая нанесённым на график точкам (с использованием вышеприведённых указаний), можно определить два параметра распределения. Если распределение действительно логарифмически-нормальное, то оно точно определяется средним геометрическим значением GM и стандартным геометрическим отклонением GSD. Значение GM соответствует вероятности 50%, и его можно получить прямо с графика как место пересечения построенной прямой линии и линии, соответствующей вероятности 50%. GSD является показателем изменчивости распределения. (При использовании графика её можно вычислить как отношение:
GSD = значение (соответствующее вероятности 84%) / значение (соответств. вероятности 16%).
Наконец, имеется проблема - как при обработке учитывать те результаты измерения, которые равны 0. Обычно в промышленной гигиене на практике те значения, которые равны 0, являются не-измеримыми значениями. Если при проведении измерений получилось много таких значений, то может потребоваться проведение анализа результатов другим способом.
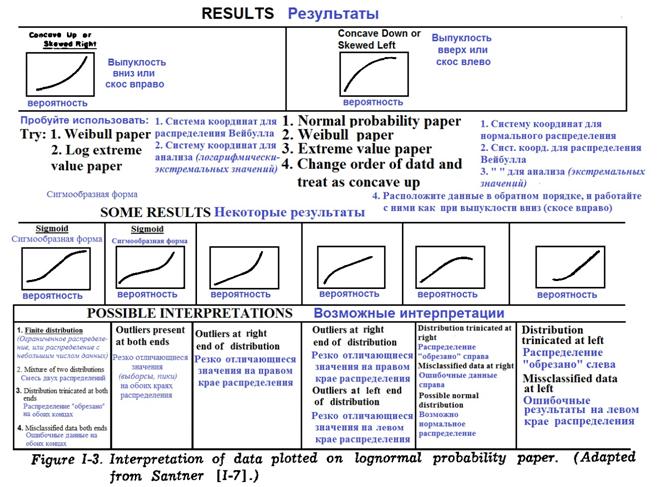
Фиг. I-3. Рекомендации по интерпретации результатов измерений, использованных при построении графика в логарифмически-нормальной системе координат
В (I-11) Berry and Day обсудили использование гамма-распределения. Перед обработкой результатов измерений рассмотрим два других возможных случая. Во-первых, если проводится анализ результатов измерения воздействия для одного рабочего места, нужно попытаться обнаружить "сгруппировывание" нулевых значений (меньших порога измерения) в определённый интервал смены. Могло случиться так, что рабочий выходил из места с загрязнённой атмосферой, или происходило изменение технологического процессе (временное).
В этом случае нулевые значения являются уже другим распределением, и их нельзя использовать при проведении анализа (остальных) значительных значений. Такое исключение результатов измерений должно проводиться с осторожностью, и (лишь) при наличии информации о перемещениях рабочего. Во-вторых, наличие маленьких воздействий может обнаружиться (при определении ряда средних значений воздействий) у тех рабочих, которые находятся в одной подгруппе по степени ожидаемого риска воздействия. Часто при проведении анализа (воздействия на рабочих) последних группируют исключительно в соответствии с названиями их специальностей - но это может привести к ошибкам. Специалист должен точно узнать, какова вероятность производственного воздействия на именно этого рабочего, прежде чем включать его в подгруппу с определённым риском воздействия,.
Но случаи, когда измеренное воздействие равно нулю (могут происходить и при иных ситуациях), и одного подходящего (универсального) способа для обработки результатов в этом случае - не существует. Один из способов - определить ''наименьшее измеримое значение'' измеримого количества загрязнений для данного метода анализа (обратившись в аналитическую лабораторию), и затем использовать это значение, заменяя им все нулевые результаты. Другой способ - устранение нулевых значений путём добавления небольшой произвольно выбранной постоянной величины ко всем нулевым значениям перед нанесением их на график.
К сожалению, иногда это можно сделать (только) методом проб и ошибок. В (I-12) Hald обсуждает добавление к результатам измерений, которые помогают проводить такое преобразование. Учтите, что выбранная постоянная величина должна быть маленькой, (чтобы) не произошло смещение среднего значения параметра распределения. (Можно, например) начать со значения, которое равно 5% от значения GSD.
Примеры - результаты измерения воздействия:
На одном и том же месте, около пульта управления, проводились последовательные измерения значений концентрации фтористого водорода (HF), получены результаты:
Результаты измерений
Ранжированные (сортированные) результаты
Время начала замеров
Концентрация, ppm
Отсортированные результаты
Положение на графике
1525
0.91
0.11
5.2%
1625
1.3
0.11
13.2%
1725
10.0
0.12
21.4%
1825
0.8
0.14
29.6%
1925
2.6
0.14
37.8%
2025
0.12
0.21
45.9%
2125
0.14
0.33
54.1%
2225
0.11
0.8
62.2%
2325
0.14
0.91
70.4%
0025
0.11
1.3
78.6%
0125
0.33
2.6
86.8%
0225
0.21
10.0
94.8%
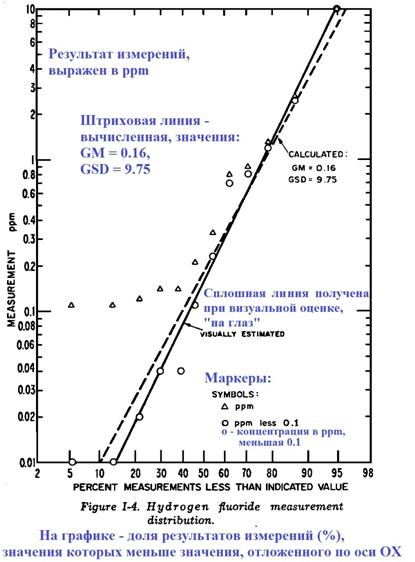
Фиг. I-4. Распределение 12 значений измеренных концентраций фтороводорода HF
Положения на графике для 12 результатов измерений (%) были получены с помощью таблицы I-1. Нанесённые на график значения показаны на Фиг. I-4. Похоже, что на левом ''конце'' графика распределение результатов отличается от логарифмически-нормального. Этот результат должен получиться, если к результатам, соответствующим логарифмически-нормальному распределению плюс случайные отклонения, добавить постоянную фоновую величину.
Результаты можно линеаризировать, если использовать трёхпараметрическую логарифмически-нормальную модель, где постоянное значение вычитается из каждого из значений перед нанесением на график. Значение этой постоянной величины (концентрации) можно оценить, используя начальный график распределения - это та концентрация, к которой асимптотически стремится график. Для Фиг. I-4 таким значением является концентрация 0.1 ppm. Поэтому значение 0.1 ppm вычитается из всех результатов перед их нанесением на график Фиг. I-4. В результате получается среднее геометрическое (взятое с графика) 0.16 ppm, что соответствует концентрации (0.16+0.1) 0.26 ppm. Значение GSD преобразованного распределения (концентрация - 0.1 ppm) вычисляется так:
GSD = (значение для вероятности 84%) / (значение для вероятности 16%) = 2.05 ppm / 0/.16 ppm = 12.8
При проведении вычислений ''напрямую'' (см. раздел 4.2.3) среднее значение Log10[концентрация - 0.1 ppm] равно -0.739, а соответствующая концентрация равна 0.28 ppm. Вычисленное значение GSD (для концентрации - 0.1 ppm) равно 9.8. Таким образом, результаты численных вычислений близки к результатам, полученным с помощью графика. Хотя первый способ предпочтительнее (он объективнее и точнее), но для практических целей точность графического способа достаточно хороша. На Фиг. I-4 штриховой линией показано распределение значений, соответствующих вычисленным величинам GM и GSD для (концентрации - 0.1 ppm).
Пример. Средние воздействия на рабочих в группе рабочих из 24 человек, специальность - ''смеситель'', воздух загрязнён метакрилатом, значения концентраций (ppm):
26, 53, 8.8, 37, 19, 31, 45, 56, 15, 49, 16, 44, 96, 39, 63, 90, 23, 16, 31, 24, 30, 24, 116, 49.
На Фиг. I-5 показан график, построенный с помощью этих значений. Используя ранее описанный метод получим (графические значения): GM = 34 ppm и GSD = 65 ppm / 34 ppm = 1.9. А при вычислениях с использованием вышеприведённых результатах измерений получим GM = 34.5 и GSD = 1.89.
Таблица I-1. Положение на оси ОХ разных точек при разном числе замеров.
Ссылки:
(1) Statistical Tables for Biological, Agricultural and Medical Research, by Fisher and Yates, Hafner pub. Co., 1963, Table XX, 94-95.
(2) Tables of Normal Probability Functions, US Governmental Printing Office, 1953, Table 1, 2-338.
(3) Pearson C and Hartley Biometrika Tables for Statisticians Volume I Cambridge University Press, 1954, Table 28, 175, Table 1 104-110.
(4) Harter M Leon Expected Values of Normal Order Statistics, ARL Technical Report 60-292, Wright-Patterson Air Force Base, July 1960.
Таблица I-1. Положение на оси ОХ разных точек при разном числе замеров - продолжение
Если число замеров больше 50, положение по оси ОХ вычисляется так:
положение = [ 100 * (порядковый номер - 0.5) ] / [ число замеров]
Пример:
Число замеров = 51,
Порядковый номер Положение по оси ОХ
1 0.98 = 100*(1-0.5)/51
2 2.94 = 100*(2-0.5)/51
… …
51 99.02 = 100*(51-0.5)/51
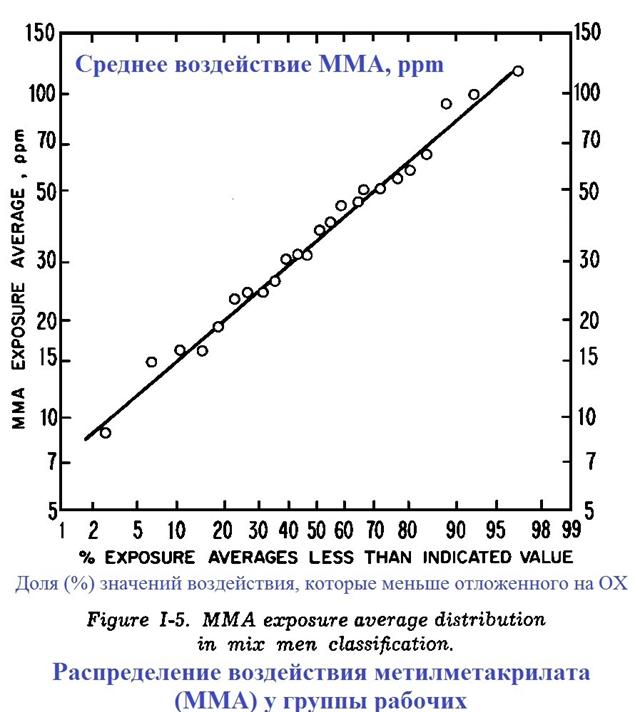
Фиг. I-5. Распределение средних воздействий метакрилата на рабочих
Ссылки
I-1. Hounam RF: An Application of the Log-Normal Distribution to Some Air Sampling Results and Recommendations on the Interpretation of Air Sampling Data. Atomic Energy Research Establishment Report AERE-M 1469. Her Majesty’s Stationery Office, London, England, 1965.
I-2. Gale HJ: The Lognormal Distribution and Some Examples of Its Application in the Field of Radiation Protection. Atomic Energy Research Establishment Report AERE-R 4736, Her Majesty’s Stationery Office, London, England, 1965.
I-3.Gale HJ. Some Examples of the Application of the Lognormal Distribution in Radiation Protection. Annals of Occupational Hygiene, 10:39-45, 1967.
I-4. Coenen W: The Confidence Limits for the Mean Values of Dust Concentration. Staub (English Translation), 26:39-45, May 1966.
I-5. Jones AR and Brief: Evaluating Benzene Exposures. American Industrial Hygiene Association Journal. 32:610-613, 1971.
I-6. Sherwood RJ: The Monitoring of Benzene Exposure by Air Sampling. American Industrial Hygiene Association Journal. 32:840-846, 1971.
I-7. Santner JF: An Introduction to Normal Probability Paper/ Environmental Control Administration Course Manual, USPHS, DHEW, Cincinnati, Ohio (unpublished).
I-8. Kottler F: The Distribution of Particle Sizes; Part II, The Probability Graphs. Journal of the Franklin Institute, 250:419-441. November 1950.
I-9. Hahn GJ and SS Shapiro: Statistical Models in Engineering. John Wiley and Sons, Inc, New York, NY 1971.
I-10. Daniel C and FS Wood: Fitting Equations to Data. Wiley-Interscience, New York, NY, 1971.
I-11. Berry G and NE Day: The Statistical Analysis of the Results of Sampling an Environment for a Contaminant When Most Samples Contain an Undetectable Level. American Journal of Epidemiology. 97(3):160-166, 1973.
I-12. Hald A: Statistical Theory with Engineering Applications. John Wiley and Sons, Inc, New York, NY 1952.



Полезная информация:
Логарифмически-нормальные графики результатов измерения воздействий и средних воздействий
Ранее, в работах (I-1 ÷ I-6) обсуждалась полезность и удобность использования (миллиметровки с логарифмически-вероятностной шкалой) для построения графиков результатов измерений воздействий в промышленной гигиене. В этом приложении рассмотрена практическая сторона использования такой бумаги. Сначала описано, как её использовать. Затем приводится два примера - измерения воздействий, и средние результаты измерений на отдельных рабочих в группе.
На Фиг. I-1 и I-2 показаны образцы такой бумаги, смеющейся в продаже (2-цикловой и 3-цикловой). Обычно она охватывает тот диапазон значений, которые получаются при измерениях. Если требуются дополнительные циклы, отрезая и приклеивая соответственные участки, можно получить бумагу с 4 или 5 циклами.
При построении графиков первым шагом является ранжирование исходных данных, чтобы они располагались в порядке возрастания значений. Обычно наименьшим значением по оси ОХ является 1, а наибольшим - n, где n - число замеров, или число средних значений воздействия. Затем ранжированные значения наносят на график. Среди специалистов по статистике нет единого мнения о том, как правильно наносить результаты на такую бумагу. Широко используемый способ предложен в (I-7). Таблица I-1 взята из этой публикации. Она охватывает число значений n от 2 до 50, и также приводится уравнение для большего числа значений.
После построения результатов и получения субъективной оценки - что результаты укладываются на прямую линию - строится линейная регрессионная линия. Важно понимать, что при использовании логарифмически-нормальных шкал нельзя применять широко известный метод наименьших квадратов. Причины этого объясняются в (I-8).
Если (регрессионная) линия хорошо соответствует результатам измерений, то (специалист) не должен считать все результаты одинаково важными (ценными). На регрессионную линию в большей степени влияют результаты, которые находятся в центре (графика). Любые отклонения, которые наблюдаются в областях с большой и с маленькой вероятностями (например - <5% и >95%) на таком графике на такой бумаге будут преувеличены, излишне подчёркнуты. Особенно - при сравнении при той же абсолютной величине отличия в средней области (например - от 20 до 80%).
Например, при вероятности 99% отклонение в 15 раз больше, чем при вероятности 50%; а при вероятности 99.5% - в 28 раз. Из-за искажений, вносимых логарифмически-нормальной шкалой, невозможно даже приблизительно (определить) величину отклонений с помощью простой проверки. Схожие примеры искажений встречаются в картографии. При использовании проекции поверхности земного шара на плоскость Меркатера искажаются расстояния между точками, конкретно - в областях около полюсов расстояния между ними возрастают.
Такая бумага должна использоваться только для нанесения результатов, и для предварительной оценки того, соответствуют ли они логарифмически-нормальной модели (распределения результатов измерений). Она также полезна, когда нужно быстро сделать оценку среднего геометрического значения (GM) и стандартного геометрического отклонения (GSD) полученной логарифмически-нормальной модели. Но такую бумагу нельзя использовать для получения статистически-обоснованных оценок того, насколько хорошо регрессионная прямая линия соответствует результатам измерений. При ''подгонке'' прямой линии к точкам (результатам измерений) наблюдается следующее:
- Игнорируются все точки, которые находятся за пределами диапазона вероятностей 1 ÷ 99%.
- Из оставшихся предпочтение отдаётся тем, которые находятся ближе к центру (50%), то есть - в диапазоне 20 ÷ 80%.
Santner в (1-7) привёл указания (Фиг. I-3), которые помогают интерпретировать информацию на графике с логарифмически-нормальной системой координат. Также предлагались другие методы линеаризации результатов и способы построения графиков.
В (I-9) Hann and Shapiro приводят полезную информацию о построении графиков в логарифмически-нормальной системе координат. Там, в главе 8 ''Probability Plotting and Testing of Distributional Assumptions'' приводится много графиков вероятностных распределений.

Фиг. I-1. Бумага с логарифмически-нормальными шкалами - двухцикловая
Там также приводятся графики, которые позволяют сравнить типичные отклонения от линейности (для графиков, построенных в логарифмически-нормальной системе координат) при использовании 20 и 50 значений (результатов измерений), взятых из разных распределений, у которых разные отклонения от нормального. При использовании (всего лишь) 20 значений, взятых из множества значений, соответствующих нормальному распределению, получаются значительные отклонения от нормального распределения (от линейности графика) из-за случайной изменчивости (взятых) значений.
В (I-10) Daniel and Wood тоже показали, какие бывают типичные отклонения от линейности из-за случайной изменчивости значений выборки. В их приложении 3А приводятся графики случайных нормальных отклонений при числе значений в выборке 8, 16, 32, 64 и 384. Они обнаружили, что при числе замеров 8 нельзя (даже) сделать выводы о том, нормально ли распределение вообще. При 16 значениях сохраняются значительные отклонения от линейности. При 32 и 64 значениях результат значительно улучшается, но продолжает не соответствовать прямой линии на ''концах'' распределения (вероятности менее 10% и более 90%).

Фиг. I-2. Бумага с логарифмически-нормальными шкалами - трёхцикловая
После того, как была построена прямая линия, наилучшим образом соответствующая нанесённым на график точкам (с использованием вышеприведённых указаний), можно определить два параметра распределения. Если распределение действительно логарифмически-нормальное, то оно точно определяется средним геометрическим значением GM и стандартным геометрическим отклонением GSD. Значение GM соответствует вероятности 50%, и его можно получить прямо с графика как место пересечения построенной прямой линии и линии, соответствующей вероятности 50%. GSD является показателем изменчивости распределения. (При использовании графика её можно вычислить как отношение:
GSD = значение (соответствующее вероятности 84%) / значение (соответств. вероятности 16%).
Наконец, имеется проблема - как при обработке учитывать те результаты измерения, которые равны 0. Обычно в промышленной гигиене на практике те значения, которые равны 0, являются не-измеримыми значениями. Если при проведении измерений получилось много таких значений, то может потребоваться проведение анализа результатов другим способом.

Фиг. I-3. Рекомендации по интерпретации результатов измерений, использованных при построении графика в логарифмически-нормальной системе координат
В (I-11) Berry and Day обсудили использование гамма-распределения. Перед обработкой результатов измерений рассмотрим два других возможных случая. Во-первых, если проводится анализ результатов измерения воздействия для одного рабочего места, нужно попытаться обнаружить "сгруппировывание" нулевых значений (меньших порога измерения) в определённый интервал смены. Могло случиться так, что рабочий выходил из места с загрязнённой атмосферой, или происходило изменение технологического процессе (временное).
В этом случае нулевые значения являются уже другим распределением, и их нельзя использовать при проведении анализа (остальных) значительных значений. Такое исключение результатов измерений должно проводиться с осторожностью, и (лишь) при наличии информации о перемещениях рабочего. Во-вторых, наличие маленьких воздействий может обнаружиться (при определении ряда средних значений воздействий) у тех рабочих, которые находятся в одной подгруппе по степени ожидаемого риска воздействия. Часто при проведении анализа (воздействия на рабочих) последних группируют исключительно в соответствии с названиями их специальностей - но это может привести к ошибкам. Специалист должен точно узнать, какова вероятность производственного воздействия на именно этого рабочего, прежде чем включать его в подгруппу с определённым риском воздействия,.
Но случаи, когда измеренное воздействие равно нулю (могут происходить и при иных ситуациях), и одного подходящего (универсального) способа для обработки результатов в этом случае - не существует. Один из способов - определить ''наименьшее измеримое значение'' измеримого количества загрязнений для данного метода анализа (обратившись в аналитическую лабораторию), и затем использовать это значение, заменяя им все нулевые результаты. Другой способ - устранение нулевых значений путём добавления небольшой произвольно выбранной постоянной величины ко всем нулевым значениям перед нанесением их на график.
К сожалению, иногда это можно сделать (только) методом проб и ошибок. В (I-12) Hald обсуждает добавление к результатам измерений, которые помогают проводить такое преобразование. Учтите, что выбранная постоянная величина должна быть маленькой, (чтобы) не произошло смещение среднего значения параметра распределения. (Можно, например) начать со значения, которое равно 5% от значения GSD.
Примеры - результаты измерения воздействия:
На одном и том же месте, около пульта управления, проводились последовательные измерения значений концентрации фтористого водорода (HF), получены результаты:
|
Результаты измерений |
Ранжированные (сортированные) результаты | ||
|
Время начала замеров |
Концентрация, ppm |
Отсортированные результаты |
Положение на графике |
|
1525 |
0.91 |
0.11 |
5.2% |
|
1625 |
1.3 |
0.11 |
13.2% |
|
1725 |
10.0 |
0.12 |
21.4% |
|
1825 |
0.8 |
0.14 |
29.6% |
|
1925 |
2.6 |
0.14 |
37.8% |
|
2025 |
0.12 |
0.21 |
45.9% |
|
2125 |
0.14 |
0.33 |
54.1% |
|
2225 |
0.11 |
0.8 |
62.2% |
|
2325 |
0.14 |
0.91 |
70.4% |
|
0025 |
0.11 |
1.3 |
78.6% |
|
0125 |
0.33 |
2.6 |
86.8% |
|
0225 |
0.21 |
10.0 |
94.8% |

Фиг. I-4. Распределение 12 значений измеренных концентраций фтороводорода HF
Положения на графике для 12 результатов измерений (%) были получены с помощью таблицы I-1. Нанесённые на график значения показаны на Фиг. I-4. Похоже, что на левом ''конце'' графика распределение результатов отличается от логарифмически-нормального. Этот результат должен получиться, если к результатам, соответствующим логарифмически-нормальному распределению плюс случайные отклонения, добавить постоянную фоновую величину.
Результаты можно линеаризировать, если использовать трёхпараметрическую логарифмически-нормальную модель, где постоянное значение вычитается из каждого из значений перед нанесением на график. Значение этой постоянной величины (концентрации) можно оценить, используя начальный график распределения - это та концентрация, к которой асимптотически стремится график. Для Фиг. I-4 таким значением является концентрация 0.1 ppm. Поэтому значение 0.1 ppm вычитается из всех результатов перед их нанесением на график Фиг. I-4. В результате получается среднее геометрическое (взятое с графика) 0.16 ppm, что соответствует концентрации (0.16+0.1) 0.26 ppm. Значение GSD преобразованного распределения (концентрация - 0.1 ppm) вычисляется так:
GSD = (значение для вероятности 84%) / (значение для вероятности 16%) = 2.05 ppm / 0/.16 ppm = 12.8
При проведении вычислений ''напрямую'' (см. раздел 4.2.3) среднее значение Log10[концентрация - 0.1 ppm] равно -0.739, а соответствующая концентрация равна 0.28 ppm. Вычисленное значение GSD (для концентрации - 0.1 ppm) равно 9.8. Таким образом, результаты численных вычислений близки к результатам, полученным с помощью графика. Хотя первый способ предпочтительнее (он объективнее и точнее), но для практических целей точность графического способа достаточно хороша. На Фиг. I-4 штриховой линией показано распределение значений, соответствующих вычисленным величинам GM и GSD для (концентрации - 0.1 ppm).
Пример. Средние воздействия на рабочих в группе рабочих из 24 человек, специальность - ''смеситель'', воздух загрязнён метакрилатом, значения концентраций (ppm):
26, 53, 8.8, 37, 19, 31, 45, 56, 15, 49, 16, 44, 96, 39, 63, 90, 23, 16, 31, 24, 30, 24, 116, 49.
На Фиг. I-5 показан график, построенный с помощью этих значений. Используя ранее описанный метод получим (графические значения): GM = 34 ppm и GSD = 65 ppm / 34 ppm = 1.9. А при вычислениях с использованием вышеприведённых результатах измерений получим GM = 34.5 и GSD = 1.89.
Таблица I-1. Положение на оси ОХ разных точек при разном числе замеров.
Ссылки:
(1) Statistical Tables for Biological, Agricultural and Medical Research, by Fisher and Yates, Hafner pub. Co., 1963, Table XX, 94-95.
(2) Tables of Normal Probability Functions, US Governmental Printing Office, 1953, Table 1, 2-338.
(3) Pearson C and Hartley Biometrika Tables for Statisticians Volume I Cambridge University Press, 1954, Table 28, 175, Table 1 104-110.
(4) Harter M Leon Expected Values of Normal Order Statistics, ARL Technical Report 60-292, Wright-Patterson Air Force Base, July 1960.
Таблица I-1. Положение на оси ОХ разных точек при разном числе замеров - продолжение
Если число замеров больше 50, положение по оси ОХ вычисляется так:
положение = [ 100 * (порядковый номер - 0.5) ] / [ число замеров]
Пример:
Число замеров = 51,
Порядковый номер Положение по оси ОХ
1 0.98 = 100*(1-0.5)/51
2 2.94 = 100*(2-0.5)/51
… …
51 99.02 = 100*(51-0.5)/51

Фиг. I-5. Распределение средних воздействий метакрилата на рабочих
Ссылки
I-1. Hounam RF: An Application of the Log-Normal Distribution to Some Air Sampling Results and Recommendations on the Interpretation of Air Sampling Data. Atomic Energy Research Establishment Report AERE-M 1469. Her Majesty’s Stationery Office, London, England, 1965.
I-2. Gale HJ: The Lognormal Distribution and Some Examples of Its Application in the Field of Radiation Protection. Atomic Energy Research Establishment Report AERE-R 4736, Her Majesty’s Stationery Office, London, England, 1965.
I-3.Gale HJ. Some Examples of the Application of the Lognormal Distribution in Radiation Protection. Annals of Occupational Hygiene, 10:39-45, 1967.
I-4. Coenen W: The Confidence Limits for the Mean Values of Dust Concentration. Staub (English Translation), 26:39-45, May 1966.
I-5. Jones AR and Brief: Evaluating Benzene Exposures. American Industrial Hygiene Association Journal. 32:610-613, 1971.
I-6. Sherwood RJ: The Monitoring of Benzene Exposure by Air Sampling. American Industrial Hygiene Association Journal. 32:840-846, 1971.
I-7. Santner JF: An Introduction to Normal Probability Paper/ Environmental Control Administration Course Manual, USPHS, DHEW, Cincinnati, Ohio (unpublished).
I-8. Kottler F: The Distribution of Particle Sizes; Part II, The Probability Graphs. Journal of the Franklin Institute, 250:419-441. November 1950.
I-9. Hahn GJ and SS Shapiro: Statistical Models in Engineering. John Wiley and Sons, Inc, New York, NY 1971.
I-10. Daniel C and FS Wood: Fitting Equations to Data. Wiley-Interscience, New York, NY, 1971.
I-11. Berry G and NE Day: The Statistical Analysis of the Results of Sampling an Environment for a Contaminant When Most Samples Contain an Undetectable Level. American Journal of Epidemiology. 97(3):160-166, 1973.
I-12. Hald A: Statistical Theory with Engineering Applications. John Wiley and Sons, Inc, New York, NY 1952.



Полезная информация: