Техническое приложение J
Доверительные пределы и уровни доверия, и их влияние рабочего и на риск рабочего
В разделе 1.5 было сказано, что из-за влияния на результат случайных погрешностей измерения полученные измеренные значения концентрации являются всего лишь оценками неизвестных правильных средних значений концентрации. Описанные в Главе 4 методы учитывают случайные отличия между истинным значением измеренного производственного воздействия и реальным воздействием. (Это позволяет) сделать (обоснованные) заявления об относительных значениях концентрации воздушных загрязнений (истинных) по отношению к ограничениям стандарта по охране труда (ПДК) - есть ли превышение ПДК. А в этом приложении обсуждается влияние выбранных уровней риска на вероятность того, что (можно будет) заявить о выполнении требований или об их нарушении. Для подготовки к обсуждению сравнения уровней риска сначала будут рассмотрены доверительные интервалы, проверка гипотез, ошибки первого и второго типов, и графики мощности критерия[1] (power function curves).
Доверительные интервалы
Методы, описанные в Главе 4, особенно - в разделах 4.2.1 и 4.2.2, являются проверками статистических гипотез в рамках (определённых) доверительных интервалов. В разделе 4.2.1 обсуждается использование одностороннего нижнего доверительного предела (LCL) и одностороннего верхнего доверительного предела (UCL) на (возможность обоснованно) заявить о выполнении требований законодательства, возможном нарушении ограничений и нарушении требований. При принятии решений о том, было ли превышение воздействия по отношению к ПДК, будет полезно изучить назначение и полезность использования доверительных интервалов.
Предположим, что у всех рабочих истинное значение средней концентрации, воздействующей на них в производственных условиях, равно 80 ppm в один определённый день. У способа отбора проб и метода анализа коэффициент изменчивости (CVt) при определении среднесменного воздействия (8-часовая смена) равен 10% - при выполнении одного непрерывного замера в течение 8 часов. Если можно сделать много одновременных замеров воздействия в течение 8-часовой смены на одного и того же рабочего в один и тот же день, то распределение результатов таких измерений будет похожим на показанное на Фиг. J-1. Конечно, специалисты по ОТ для определения среднего воздействия на рабочих обычно делают по одному замеру в день. на основе реально сделанных измерений, мы хотим сделать (обоснованное) количественное заявление о значении неизвестного нам среднего истинного воздействия.
Показанное на Фиг. J-1 распределение результатов измерений даёт нам относительные частоты многих возможных значений, которые мы можем получить при проведении одного измерения. Около 68% возможных значений находится в диапазоне, расположенного около ''центрального'' значения - истинного, от 72 ppm (μ-σ) до 88 ppm (μ+σ). Таким образом, с вероятностью 68% результат одиночного измерения окажется в интервале ±10% (8 ppm) от истинного значения (80 ppm).
Но в одной трети случаев, из-за случайных погрешностей, он будет попадать за пределы этого узкого интервала (в центре). В диапазон от 64.3 ppm (μ-1.96*σ) до 95.7 ppm (μ+1.96*σ) попадёт 95% от всех возможных значений результатов измерений. Как было показано в приложении D, поскольку проводились однократные замеры в течение 8 часов непрерывно, то у этого метода отбора проб и анализа при доверительном уровне 95% погрешность составляет 20% (1.96*CVt) - так как результаты такого замера должны находиться в пределах ± 20% от истинного воздействия в течение 95% времени.
Всегда неизвестно - какое же воздействие было на самом деле. Но нам известен коэффициент изменчивости метода отбора проб и их анализа CVt, число замеров (в рассматриваемом случае - один), и мы предполагаем, что распределение погрешностей соответствует нормальному закону (как показано на Фиг. J-1). Используя эту информацию, мы можем вычислить доверительные интервалы, ограничивающие с двух сторон интервалы значений, находящихся около измеренных значений так, что эти интервалы будут, вероятно, содержать истинное значение воздействия. (Из-за) большой вероятности того, что эти интервалы будут содержать истинные значения воздействия, их называют доверительными.
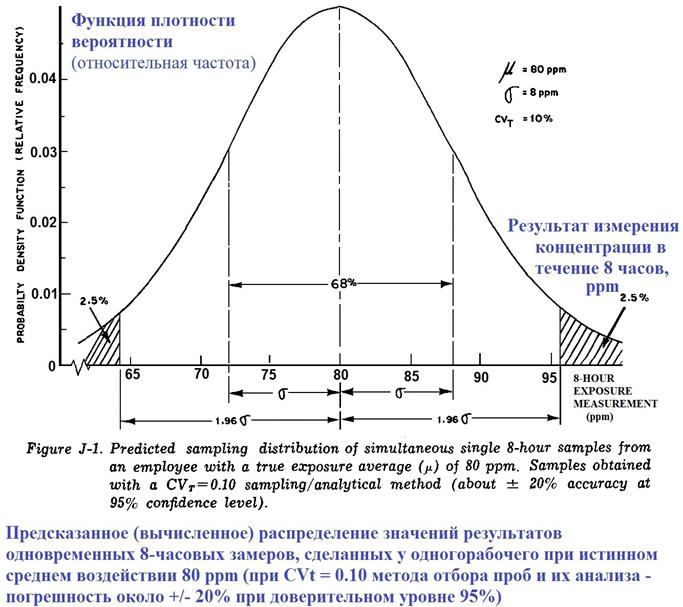
Фиг. J-1. Предсказанное распределение результатов измерений, которые получатся при одновременном проведении замеров у одного и того же рабочего 8 часов непрерывно (одиночный замер) у рабочего, у которого истинное среднее воздействие (μ) равно 80 ppm. Коэффициент изменчивости метода отбора проб и их анализа CVt = 0.10 (погрешность около ±20% при 95% уровне доверия).
В Natrella (J-1) приводится несколько иллюстраций (Фиг. 1-8 - 1-10), которые показывают это. Обычно при вычислении этих пределов мы выбираем доверительный коэффициент 0.95 (уровень доверия 95%). Слово ''вероятность'', которое используется здесь вместе с доверительными пределами, относится к относительной частоте (то есть - к доле случаев), когда на практике в границы доверительных пределов попадает истинное значение воздействия. Таким образом ожидается, что при проведении большого числа измерений 95% вычисленных доверительных интервалов будут содержать соответствующие истинные значения воздействия. Поэтому - так как мы проводим только одно измерение - вычисленные двусторонние доверительные интервалы не будут содержать истинное среднее значение воздействия с вероятностью 5%.
Иногда важно определить верхнюю границу возможных истинных значений воздействия, которая не будет превышена на практике с большой вероятностью (истинное среднее значение), или нижнюю границу истинных воздействий, которая с большой вероятностью будет будет ниже истинного значения. Пример использования верхней границы - мы можем захотеть, чтобы истинное среднее значение воздействия оказалось ниже ПДК (TLV) в 19 случаях из 20. Чтобы (успешно) пройти проверку, 95% односторонний доверительный предел должен быть меньше значения ПДК. Этот подход использован в разделе 4.1.
В целом об использовании доверительных пределов можно сказать следующее. Мы видим, что (из-за непостоянства воздействия) недостаточно сказать, что значение среднего истинного воздействия схоже с измеренным средним значением. (Применяя информацию о погрешности методов отбора проб и анализа), мы используем распределение значений измеренных воздействий для того, чтобы получить или двусторонний доверительный интервал (относительно среднего измеренного значения), или односторонний доверительный интервал (то есть - верхнюю или нижнюю границу) с одной стороны от измеренного среднего значения.
Затем мы можем сказать, что (с выбранным уровнем доверия) двусторонний интервал (или же односторонний интервал) содержит истинное среднее значение воздействия. А вероятность того, что мы проведём измерения так неудачно, что результат измерений будет настолько сильно отличаться от истинного значения, что последнее не попадёт в доверительный интервал - это уровень риска (данного) доверительного интервала. Использованный здесь термин ''уровень риска'' означает вероятность, дополняющую уровень доверия до 100%. То есть, при 95% доверительном интервале уровень риска будет 5% (вероятность того,что истинное значение не попадёт в интервал = 100% - 95% = 5%).
Проверка значимости, или проверка гипотез
Принятие решений в Главе 4 основано на доверительных интервалах, которые алгебраически эквивалентны соответствующей статистической проверке значимости. Полезно рассмотреть используемую терминологию и проверку гипотез, и сравнить их с принятием решений с помощью доверительных интервалов.
Промышленному гигиенисту нужно проверить гипотезы, которые относятся к сравнению друг с другом истинных значений воздействия и установленных значений ПДК. В этом случае, гипотезой является предположение о значении (state) истинного среднего воздействия μ. Проверки статистической значимости рассматривают две гипотезы. Перед проведением измерений делается предварительное предположение о значении полного среднего воздействия по отношению к ПДК. Затем если статистическая проверка не покажет ошибочность предварительного предположения, оно принимается, Под ошибочностью мы имеем в виду, что вероятность того, что сделанные измерения окажутся соответствующими сделанным предварительным предположениям, будет низкой (например - меньше 5%). Эта предварительная отрицательная гипотеза называется нулевой гипотезой. Соответственно делается альтернативное - противоположное предположение. Такое предположение принимается тогда, когда нулевая гипотеза отбрасывается. Эти гипотезы основаны на том подходе, который использует промышленный гигиенист. Подходы, используемые работодателем и инспектором (по охране труда) - отличаются (от вышеописанных), и они будут рассмотрены ниже.
Подход работодателя
Каждый работодатель обязан обеспечить каждого своего работника безопасными и здоровыми условиями труда так, чтобы отсутствовали известные вредные факторы, которые могут привести к смерти или серьёзному повреждению здоровья. Для этого работодатель должен обеспечить снижение реального воздействия на сотрудника до уровня, меньшего соответствующей ПДК. Таким образом, работодатель должен принимать решения при оценке результатов измерений так, чтобы он был уверен, что у него нет сотрудников, воздействие на которых превышает (среднесменные) ПДК, и что у него нет сотрудников, воздействие на которых превышает (краткосрочные) ПДК в любой момент времени.
Со статистической точки зрения, работодатель должен сформулировать нулевую гипотезу о том, что реальное воздействие превышает ПДК, и возложить ''бремя доказывания'' на результаты измерений, которые могут показать выполнение требований с учётом изменчивости результатов измерений. Для проверки работодателем выполнения требований законодательства:
Нулевая гипотеза Но: μ > ПДК - нарушение требований;
Альтернативная гипотеза На: μ ≤ ПДК - выполнение требований законодательства.
Подход инспектора по ОТ
Государственная инспекция должна выполнить проверку выполнения требований законодательства так, чтобы её результаты проверки были обоснованы. То есть, она должна доказать, что в день проведения замеров произошло превышение ПДК. Это связано с тем, что стандарты OSHA относятся или к среднесменному воздействию (за 8 часов), или ограничивают кратковременное воздействие, которое не должно превышаться ни разу в течение смены (стандарт 29 CFR 1910.1000). Таким образом, инспектор должен сформулировать нулевую и альтернативную гипотезы так, чтобы (использованные) результаты измерений могли показать нарушение требований законодательства с учётом случайной погрешности результатов измерений. Для инспектора - проверка нарушения требований законодательства:
Нулевая гипотеза Но: μ ≤ ПДК - выполнение требований законодательства;
Альтернативная гипотеза На: μ > ПДК - нарушение требований.
Ошибки при проверке гипотез
Когда мы используем доверительный интервал как критерий для измеренных средних значений (Х*), мы сознаём, что есть риск, что в доверительный интервал не попадёт значение истинного среднего воздействия. При проверке гипотез используют термины: ошибка первого рода и ошибка второго рода. Эти термины относятся к двум видам ошибочных решений, которые мы можем сделать на основании результатов наших измерений и проверок. Если мы отвергнем нулевую гипотезу (и примем альтернативную гипотезу) в случае, когда верна именно нулевая гипотеза, то мы совершим ошибку первого рода. С другой стороны, если мы не отвергнем нулевую гипотезу, когда она на самом деле ошибочна, то мы совершим ошибку второго рода.
В таблице приведена информация о проверке гипотез работодателем и инспектором
Проверка инспектором нарушения требований законодательства
Реальное состояние дел
Результат проверки
Требования выполняются
Требования не выполняются
Принято решение о отсутствии нарушений
Нет ошибок
Ошибка второго рода
Принято решение о наличии нарушений
Ошибка первого рода
Нет ошибок
Проверка работодателем выполнения требований законодательства
Реальное состояние дел
Результат проверки
Требования выполняются
Требования не выполняются
Принято решение о отсутствии нарушений
Нет ошибок
Ошибка первого рода
Принято решение о наличии нарушений
Ошибка второго рода
Нет ошибок
Чтобы прояснить интерпретацию принятия статистических решений, мы будем обсуждать приведённую таблицу, используя то, что относится к инспектору. В Главе 4 мы сформулировали критерии принятия решений инспектором:
Отбрасывание Но: μ ≤ ПДК, и
Принятие Ho: μ > ПДК - всякий раз, когда доверительный интервал для истинного среднего значения при уровне доверия 100(1-α)% не включает в себя значение 1 ПДК.



Полезная информация:
Доверительные пределы и уровни доверия, и их влияние рабочего и на риск рабочего
В разделе 1.5 было сказано, что из-за влияния на результат случайных погрешностей измерения полученные измеренные значения концентрации являются всего лишь оценками неизвестных правильных средних значений концентрации. Описанные в Главе 4 методы учитывают случайные отличия между истинным значением измеренного производственного воздействия и реальным воздействием. (Это позволяет) сделать (обоснованные) заявления об относительных значениях концентрации воздушных загрязнений (истинных) по отношению к ограничениям стандарта по охране труда (ПДК) - есть ли превышение ПДК. А в этом приложении обсуждается влияние выбранных уровней риска на вероятность того, что (можно будет) заявить о выполнении требований или об их нарушении. Для подготовки к обсуждению сравнения уровней риска сначала будут рассмотрены доверительные интервалы, проверка гипотез, ошибки первого и второго типов, и графики мощности критерия[1] (power function curves).
Доверительные интервалы
Методы, описанные в Главе 4, особенно - в разделах 4.2.1 и 4.2.2, являются проверками статистических гипотез в рамках (определённых) доверительных интервалов. В разделе 4.2.1 обсуждается использование одностороннего нижнего доверительного предела (LCL) и одностороннего верхнего доверительного предела (UCL) на (возможность обоснованно) заявить о выполнении требований законодательства, возможном нарушении ограничений и нарушении требований. При принятии решений о том, было ли превышение воздействия по отношению к ПДК, будет полезно изучить назначение и полезность использования доверительных интервалов.
Предположим, что у всех рабочих истинное значение средней концентрации, воздействующей на них в производственных условиях, равно 80 ppm в один определённый день. У способа отбора проб и метода анализа коэффициент изменчивости (CVt) при определении среднесменного воздействия (8-часовая смена) равен 10% - при выполнении одного непрерывного замера в течение 8 часов. Если можно сделать много одновременных замеров воздействия в течение 8-часовой смены на одного и того же рабочего в один и тот же день, то распределение результатов таких измерений будет похожим на показанное на Фиг. J-1. Конечно, специалисты по ОТ для определения среднего воздействия на рабочих обычно делают по одному замеру в день. на основе реально сделанных измерений, мы хотим сделать (обоснованное) количественное заявление о значении неизвестного нам среднего истинного воздействия.
Показанное на Фиг. J-1 распределение результатов измерений даёт нам относительные частоты многих возможных значений, которые мы можем получить при проведении одного измерения. Около 68% возможных значений находится в диапазоне, расположенного около ''центрального'' значения - истинного, от 72 ppm (μ-σ) до 88 ppm (μ+σ). Таким образом, с вероятностью 68% результат одиночного измерения окажется в интервале ±10% (8 ppm) от истинного значения (80 ppm).
Но в одной трети случаев, из-за случайных погрешностей, он будет попадать за пределы этого узкого интервала (в центре). В диапазон от 64.3 ppm (μ-1.96*σ) до 95.7 ppm (μ+1.96*σ) попадёт 95% от всех возможных значений результатов измерений. Как было показано в приложении D, поскольку проводились однократные замеры в течение 8 часов непрерывно, то у этого метода отбора проб и анализа при доверительном уровне 95% погрешность составляет 20% (1.96*CVt) - так как результаты такого замера должны находиться в пределах ± 20% от истинного воздействия в течение 95% времени.
Всегда неизвестно - какое же воздействие было на самом деле. Но нам известен коэффициент изменчивости метода отбора проб и их анализа CVt, число замеров (в рассматриваемом случае - один), и мы предполагаем, что распределение погрешностей соответствует нормальному закону (как показано на Фиг. J-1). Используя эту информацию, мы можем вычислить доверительные интервалы, ограничивающие с двух сторон интервалы значений, находящихся около измеренных значений так, что эти интервалы будут, вероятно, содержать истинное значение воздействия. (Из-за) большой вероятности того, что эти интервалы будут содержать истинные значения воздействия, их называют доверительными.

Фиг. J-1. Предсказанное распределение результатов измерений, которые получатся при одновременном проведении замеров у одного и того же рабочего 8 часов непрерывно (одиночный замер) у рабочего, у которого истинное среднее воздействие (μ) равно 80 ppm. Коэффициент изменчивости метода отбора проб и их анализа CVt = 0.10 (погрешность около ±20% при 95% уровне доверия).
В Natrella (J-1) приводится несколько иллюстраций (Фиг. 1-8 - 1-10), которые показывают это. Обычно при вычислении этих пределов мы выбираем доверительный коэффициент 0.95 (уровень доверия 95%). Слово ''вероятность'', которое используется здесь вместе с доверительными пределами, относится к относительной частоте (то есть - к доле случаев), когда на практике в границы доверительных пределов попадает истинное значение воздействия. Таким образом ожидается, что при проведении большого числа измерений 95% вычисленных доверительных интервалов будут содержать соответствующие истинные значения воздействия. Поэтому - так как мы проводим только одно измерение - вычисленные двусторонние доверительные интервалы не будут содержать истинное среднее значение воздействия с вероятностью 5%.
Иногда важно определить верхнюю границу возможных истинных значений воздействия, которая не будет превышена на практике с большой вероятностью (истинное среднее значение), или нижнюю границу истинных воздействий, которая с большой вероятностью будет будет ниже истинного значения. Пример использования верхней границы - мы можем захотеть, чтобы истинное среднее значение воздействия оказалось ниже ПДК (TLV) в 19 случаях из 20. Чтобы (успешно) пройти проверку, 95% односторонний доверительный предел должен быть меньше значения ПДК. Этот подход использован в разделе 4.1.
В целом об использовании доверительных пределов можно сказать следующее. Мы видим, что (из-за непостоянства воздействия) недостаточно сказать, что значение среднего истинного воздействия схоже с измеренным средним значением. (Применяя информацию о погрешности методов отбора проб и анализа), мы используем распределение значений измеренных воздействий для того, чтобы получить или двусторонний доверительный интервал (относительно среднего измеренного значения), или односторонний доверительный интервал (то есть - верхнюю или нижнюю границу) с одной стороны от измеренного среднего значения.
Затем мы можем сказать, что (с выбранным уровнем доверия) двусторонний интервал (или же односторонний интервал) содержит истинное среднее значение воздействия. А вероятность того, что мы проведём измерения так неудачно, что результат измерений будет настолько сильно отличаться от истинного значения, что последнее не попадёт в доверительный интервал - это уровень риска (данного) доверительного интервала. Использованный здесь термин ''уровень риска'' означает вероятность, дополняющую уровень доверия до 100%. То есть, при 95% доверительном интервале уровень риска будет 5% (вероятность того,что истинное значение не попадёт в интервал = 100% - 95% = 5%).
Проверка значимости, или проверка гипотез
Принятие решений в Главе 4 основано на доверительных интервалах, которые алгебраически эквивалентны соответствующей статистической проверке значимости. Полезно рассмотреть используемую терминологию и проверку гипотез, и сравнить их с принятием решений с помощью доверительных интервалов.
Промышленному гигиенисту нужно проверить гипотезы, которые относятся к сравнению друг с другом истинных значений воздействия и установленных значений ПДК. В этом случае, гипотезой является предположение о значении (state) истинного среднего воздействия μ. Проверки статистической значимости рассматривают две гипотезы. Перед проведением измерений делается предварительное предположение о значении полного среднего воздействия по отношению к ПДК. Затем если статистическая проверка не покажет ошибочность предварительного предположения, оно принимается, Под ошибочностью мы имеем в виду, что вероятность того, что сделанные измерения окажутся соответствующими сделанным предварительным предположениям, будет низкой (например - меньше 5%). Эта предварительная отрицательная гипотеза называется нулевой гипотезой. Соответственно делается альтернативное - противоположное предположение. Такое предположение принимается тогда, когда нулевая гипотеза отбрасывается. Эти гипотезы основаны на том подходе, который использует промышленный гигиенист. Подходы, используемые работодателем и инспектором (по охране труда) - отличаются (от вышеописанных), и они будут рассмотрены ниже.
Подход работодателя
Каждый работодатель обязан обеспечить каждого своего работника безопасными и здоровыми условиями труда так, чтобы отсутствовали известные вредные факторы, которые могут привести к смерти или серьёзному повреждению здоровья. Для этого работодатель должен обеспечить снижение реального воздействия на сотрудника до уровня, меньшего соответствующей ПДК. Таким образом, работодатель должен принимать решения при оценке результатов измерений так, чтобы он был уверен, что у него нет сотрудников, воздействие на которых превышает (среднесменные) ПДК, и что у него нет сотрудников, воздействие на которых превышает (краткосрочные) ПДК в любой момент времени.
Со статистической точки зрения, работодатель должен сформулировать нулевую гипотезу о том, что реальное воздействие превышает ПДК, и возложить ''бремя доказывания'' на результаты измерений, которые могут показать выполнение требований с учётом изменчивости результатов измерений. Для проверки работодателем выполнения требований законодательства:
Нулевая гипотеза Но: μ > ПДК - нарушение требований;
Альтернативная гипотеза На: μ ≤ ПДК - выполнение требований законодательства.
Подход инспектора по ОТ
Государственная инспекция должна выполнить проверку выполнения требований законодательства так, чтобы её результаты проверки были обоснованы. То есть, она должна доказать, что в день проведения замеров произошло превышение ПДК. Это связано с тем, что стандарты OSHA относятся или к среднесменному воздействию (за 8 часов), или ограничивают кратковременное воздействие, которое не должно превышаться ни разу в течение смены (стандарт 29 CFR 1910.1000). Таким образом, инспектор должен сформулировать нулевую и альтернативную гипотезы так, чтобы (использованные) результаты измерений могли показать нарушение требований законодательства с учётом случайной погрешности результатов измерений. Для инспектора - проверка нарушения требований законодательства:
Нулевая гипотеза Но: μ ≤ ПДК - выполнение требований законодательства;
Альтернативная гипотеза На: μ > ПДК - нарушение требований.
Ошибки при проверке гипотез
Когда мы используем доверительный интервал как критерий для измеренных средних значений (Х*), мы сознаём, что есть риск, что в доверительный интервал не попадёт значение истинного среднего воздействия. При проверке гипотез используют термины: ошибка первого рода и ошибка второго рода. Эти термины относятся к двум видам ошибочных решений, которые мы можем сделать на основании результатов наших измерений и проверок. Если мы отвергнем нулевую гипотезу (и примем альтернативную гипотезу) в случае, когда верна именно нулевая гипотеза, то мы совершим ошибку первого рода. С другой стороны, если мы не отвергнем нулевую гипотезу, когда она на самом деле ошибочна, то мы совершим ошибку второго рода.
В таблице приведена информация о проверке гипотез работодателем и инспектором
|
Проверка инспектором нарушения требований законодательства | ||
|
|
Реальное состояние дел | |
|
Результат проверки |
Требования выполняются |
Требования не выполняются |
|
Принято решение о отсутствии нарушений |
Нет ошибок |
Ошибка второго рода |
|
Принято решение о наличии нарушений |
Ошибка первого рода |
Нет ошибок |
|
Проверка работодателем выполнения требований законодательства | ||
|
|
Реальное состояние дел | |
|
Результат проверки |
Требования выполняются |
Требования не выполняются |
|
Принято решение о отсутствии нарушений |
Нет ошибок |
Ошибка первого рода |
|
Принято решение о наличии нарушений |
Ошибка второго рода |
Нет ошибок |
Чтобы прояснить интерпретацию принятия статистических решений, мы будем обсуждать приведённую таблицу, используя то, что относится к инспектору. В Главе 4 мы сформулировали критерии принятия решений инспектором:
Отбрасывание Но: μ ≤ ПДК, и
Принятие Ho: μ > ПДК - всякий раз, когда доверительный интервал для истинного среднего значения при уровне доверия 100(1-α)% не включает в себя значение 1 ПДК.



Полезная информация: