Техническое приложение J
Доверительные пределы и уровни доверия, и их влияние рабочего и на риск рабочего
Риск (вероятность) совершить ошибку первого рода обозначается α. Максимальное значение α - это уровень значимости проверки. Заметим, что уровень доверия (1-α) является величиной, дополняющей α (для ошибки первого рода) до 100%. Это так, поскольку при принятии решения мы используем доверительный интервал, а он по своей формулировке алгебраически эквивалентен уровню значимости α при проверке нулевой гипотезы Но, таким образом, принятие решений на основе 95% доверительного интервала - это то же самое,что и проверка значимости с 5% максимальным риском (вероятностью) совершить ошибку первого рода.
Риск совершить ошибку второго рода обозначается β. Значение β изменяется в зависимости от величины реальных отличий между ПДК и истинным средним воздействием. Взаимосвязь между этими двумя видами риска показана или на графике функции мощности проверки (мощности критерия[2]), или на кривой оперативной характеристики (см. ту же сноску), обсуждаемой ниже. (Статистическая) мощность проверки (мощность критерия) - это вероятность принять альтернативную гипотезу в том случае, когда она верна. Эта (статистическая) мощность обозначается (1-β), и она дополняет вероятность совершить ошибку второго рода (β) до 100%.
Взаимосвязь доверительных пределов и проверок значимости
Эквивалентность проверок, описанных в Главе 4 и соответствующих проверок значимости показана выше, и в этом приложении не приводится. Достаточно сказать, что (используемые) нами правила принятия решений эквивалентны проверки значимости нулевой гипотезы,приведённым выше. В главе 21 в (J-1) приводится обсуждение сравнения двух этих подходов. Мы предпочитаем использовать односторонние пределы - верхний и нижний - так как величина отличия между этим пределом и ПДК позволяет оценить, насколько обоснованно принятое нами решение. Для дополнительного изучения этих вопросов рекомендуем: Bowker and Liberman (J-2), Crow et al (J-3) и Snedecor and Cochran (J-4).
Графики функции мощности проверки
Ранее термин "95% уровень доверия" использовался для проверки статистических гипотез. Этот термин появился из-за того, что используется 5% уровень риска в эквивалентной статистической проверке гипотез. Очевидным преимуществом использования статистических проверок для принятия решения о соответствии требований законодательства является то, что можно заранее выбрать максимальный желаемый уровень риска, и вычислить кривые функции мощности критерия. Эти графики дают значения мощности проверки (1-β) как функции от истинного среднего μ. Barlett and Provost в (J-5) показали, как можно пятью различными способами интерпретировать стандарты, уровни риска и др. Работодатели, инспектора и рабочие по-разному могут интерпретировать (вышеперечисленное). Интерпретация затрагивает размер выборки, выбранные уровни доверия или риска, и критерия принятия или отвержения (гипотез).
Для иллюстрации разных интерпретаций можно использовать графики функции мощности (критерия) для каждой проверки. Функция мощности дополняет функцию оперативной характеристики. В Natrella (J-1) и Bowkker and Lieberman (J-2) приводятся кривые оперативных характеристик для многих обычных (стандартных) статистических проверок. Мы будем вычислять схожую функции мощности для проверок из разделов 4.2.1 и 4.2.2. При выполнении этих проверках предполагается, что при проверке нулевой гипотезы CVt известен без погрешности, (и) что истинное среднее значение равно ПДК. Таким образом, значение 1.645*CVt* √(n) является мерой погрешности отбора проб и метода их анализа (у измеренного среднего значения стандартизованной концентрации).
Точнее - в этой формуле 1.645 является 95% перцентилью стандартизованного нормального распределения. Для получения верхнего одностороннего предела - 95%-го доверительного предела для истинной средней стандартизованной концентрации - вычисленное с помощью этой формулы значение добавляется к среднему измеренному значению (или же, для получения нижнего одностороннего предела, оно вычитается из среднего измеренного значения) в соответствии с разделами 4.2.1 и 4.2.2. (Для обсуждения значения используемого термина "уровень доверия" обратитесь к (cтатистическим замечаниям в 4.2.1.).
Если учитывать, что имеется погрешность как при определении среднего значения стандартизованного воздействия ẍ, так и при определении Cvt, то можно вычислить более точное значение 95% предела погрешности. (значения CVt, приведённые в техническом приложении D для методов отбора проб и их анализа NIOSH, были получены для 6 замеров для каждой из трёх концентраций загрязнений). Если это сделать, то коэффициент 1.645 для большинства из методов нужно будет увеличить примерно на 10%, чтобы учесть неопределённость экспериментально полученных значений CVt.
Но точный множитель, который нужно умножить на коэффициент 1.645 пока ещё нельзя вычислить, так как наши CVt определены при проведении измерений при тщательно контролируемом расходе воздуха при использовании критического отверстия. Значения CV для дополнительной погрешности (в производственных условиях) вызванные использованием индивидуального пробоотборного насоса (обозначаются CVр) были добавлены для получения консервативных значений CVt в техническом приложении D.
Мы используем CVt как известную величину[3], и используем нормальное распределение (а не Student-t) как основу для проверки статистики и для соответствующих функций мощности, приводимых ниже. Мы считаем, что при внесении (дополнительных) поправок с использованием результатов экспериментальных измерений CVp вместо 0.05, общий эффект такого уточнения пренебрежимо мал, поскольку ожидается, что две поправки дают вклад в противоположных направлениях.
Значение коэффициента 1.645 немного возрастёт, но оценка CVp (это компонент CVt), как ожидается, будет меньше, чем 0.05. В целом, мы считаем, что статистические проверки, описанные в разделах 4.2.1 и 4.2.2, а также графики функции мощности, приведённые в этом разделе - достаточно точные. Но - до тех пор, пока не будут получены более точные экспериментальные оценки погрешности пробоотборного насоса, - "половину ширины" доверительного интервала можно увеличить на примерно 10% (то есть - использовать 1.81 вместо 1.645).
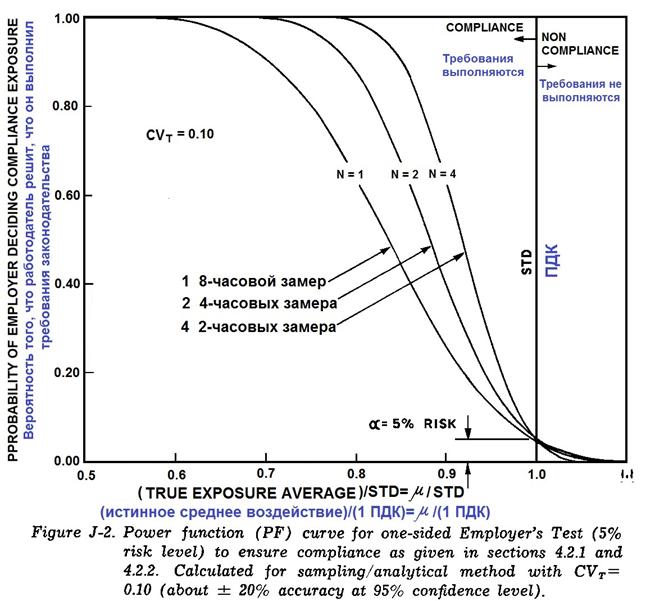
Фиг. J-2. График функции мощности (критерия) для одностороннего интервала (при проверке работодателем и 5% уровне риска) для проверки выполнения требований законодательства согласно указаниям разделов 4.2.1 и 4.2.2. Вычисления проводились для коэффициента
Ниже приводится обсуждение вычисления кривых мощности. На Фиг. J-2 (графики приводятся) для проверки работодателем выполнения требований; статистическая проверка (согласно раздела 4.2.2.1) - верхний доверительный предел (95%):
UCL(95%) = ẍ+ [ 1/645*CVt ] / √(n)
где 1.645 является коэффициентом для одностороннего 95% предела у нормального распределения.
Если верхний доверительный предел UCL меньше 1, то результатом проведённой проверки является отбрасывание нулевой гипотезы Но о нарушении требований законодательства, и принятие альтернативной гипотезы На. Эквивалентным правилом для принятия решения является:
{ ẍ } < { 1 - [1.645*Cvt]/ √(n) } для выполнения требований законодательства.
Пример:
Для одиночного 8-часового замера (n=1) и CVt = 0.10 для выполнения требований необходимо, чтобы выполнялось условие:
{ ẍ } < { 0.8355 }
Для (получения) графика функции мощности (критерия) мы должны рассмотреть все возможные стандартизованные значения измеренных средних стандартизованных значений ẍ, которые могут быть получены, и те из них, которые могут привести к отбрасыванию нулевой гипотезы. Пусть истинное среднее стандартизованное воздействие μ/STD равно 0.9, то есть - что воздействие на рабочего меньше ПДК с запасом 10%. Когда мы проверяем нулевую гипотезу о нарушении требований законодательства, мощностью проверки будет вероятность того, что проверка результатов покажет выполнение требований, то есть - отвергнет нулевую гипотезу. Вероятность отбрасывания Но равна:
Вероятность [ ẍ < 0.8355 ]
Мы вычисляем стандартную нормальную переменную:
z = { 0.8355 - 0.9} / { CVt / √(n) } = -0.0645 / [ 0.10 / √(1) ] = -0.645
Вероятность отвергнуть Но - это вероятность получить значение, меньшее чем (-0.645) с помощью стандартного нормального распределения (среднее значение равно 0, изменчивость 1).
Вероятность { z < (-0.645) } ≈ 0.26
При таком подходе стандартизованное нормальное распределение было использовано для вычисления графиков, показанных на Фиг. J-2 ÷ J-6. Для вычислений использовали калькулятор Wang 2200 и программу PS.01-2200.01A-00f1-16-0 для вычисления интегралов нормального распределения.
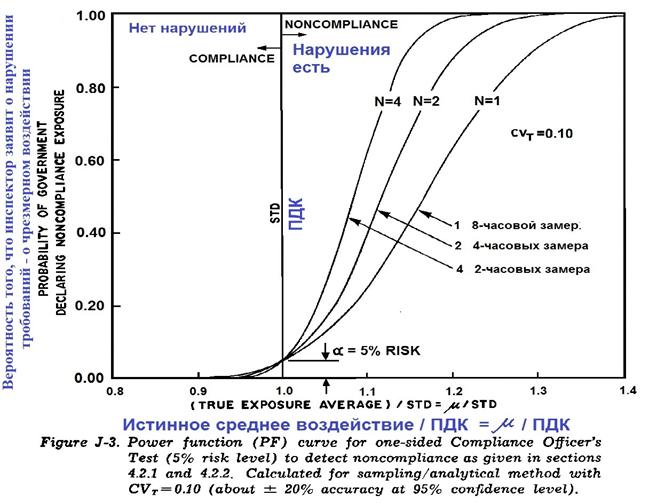
Фиг. J-3. График функции мощности (критерия) для одностороннего интервала (при проверке инспектором и 5% уровне риска) для проверки нарушения требований законодательства согласно указаниям разделов 4.2.1 и 4.2.2. Вычисления проводились для коэффициента изменчивости отбора проб и их анализа CVt = 0.10 (погрешность около ± 20% при уровне доверия 95%).
Сравнение функций мощности для проверок,проводимых инспектором,
при уровнях значимости 1% и 5%
Для инспектора графики функции мощности (критерия) дают мощность (вероятность) того, что результаты измерений показывают нарушение требований, когда такое нарушение действительно существует. На Фиг. J-3 приводится график для проверки, проводимой инспектором, при уровне значимости (риске) 5%. Критерий (в этом случае) - повестка в суд не должна оформляться, если нижний 95% односторонний доверительный предел (95% LCL) значения воздействия на рабочего не превысил ПДК.
Так как вероятность ошибки первого рода 5%, может ли работодатель заявить,что его некорректно обвиняют в течение 5% времени? Конечно нет. Только в том случае, если истинное среднее воздействие на рабочего, у которого проводились измерения, немножко меньше ПДК, имеется вероятность 5% того, что будет ошибочно оформлена повестка в суд, и эта (вероятность) быстро снижается почти до нуля при истинных значениях воздействия на рабочих, меньших ПДК. Термин "5%-й уровень риска" относится к максимальному риску заявить о нарушении требований законодательства в случае, когда истинное среднее воздействие на рабочего почти равно ПДК.



Полезная информация:
Доверительные пределы и уровни доверия, и их влияние рабочего и на риск рабочего
Риск (вероятность) совершить ошибку первого рода обозначается α. Максимальное значение α - это уровень значимости проверки. Заметим, что уровень доверия (1-α) является величиной, дополняющей α (для ошибки первого рода) до 100%. Это так, поскольку при принятии решения мы используем доверительный интервал, а он по своей формулировке алгебраически эквивалентен уровню значимости α при проверке нулевой гипотезы Но, таким образом, принятие решений на основе 95% доверительного интервала - это то же самое,что и проверка значимости с 5% максимальным риском (вероятностью) совершить ошибку первого рода.
Риск совершить ошибку второго рода обозначается β. Значение β изменяется в зависимости от величины реальных отличий между ПДК и истинным средним воздействием. Взаимосвязь между этими двумя видами риска показана или на графике функции мощности проверки (мощности критерия[2]), или на кривой оперативной характеристики (см. ту же сноску), обсуждаемой ниже. (Статистическая) мощность проверки (мощность критерия) - это вероятность принять альтернативную гипотезу в том случае, когда она верна. Эта (статистическая) мощность обозначается (1-β), и она дополняет вероятность совершить ошибку второго рода (β) до 100%.
Взаимосвязь доверительных пределов и проверок значимости
Эквивалентность проверок, описанных в Главе 4 и соответствующих проверок значимости показана выше, и в этом приложении не приводится. Достаточно сказать, что (используемые) нами правила принятия решений эквивалентны проверки значимости нулевой гипотезы,приведённым выше. В главе 21 в (J-1) приводится обсуждение сравнения двух этих подходов. Мы предпочитаем использовать односторонние пределы - верхний и нижний - так как величина отличия между этим пределом и ПДК позволяет оценить, насколько обоснованно принятое нами решение. Для дополнительного изучения этих вопросов рекомендуем: Bowker and Liberman (J-2), Crow et al (J-3) и Snedecor and Cochran (J-4).
Графики функции мощности проверки
Ранее термин "95% уровень доверия" использовался для проверки статистических гипотез. Этот термин появился из-за того, что используется 5% уровень риска в эквивалентной статистической проверке гипотез. Очевидным преимуществом использования статистических проверок для принятия решения о соответствии требований законодательства является то, что можно заранее выбрать максимальный желаемый уровень риска, и вычислить кривые функции мощности критерия. Эти графики дают значения мощности проверки (1-β) как функции от истинного среднего μ. Barlett and Provost в (J-5) показали, как можно пятью различными способами интерпретировать стандарты, уровни риска и др. Работодатели, инспектора и рабочие по-разному могут интерпретировать (вышеперечисленное). Интерпретация затрагивает размер выборки, выбранные уровни доверия или риска, и критерия принятия или отвержения (гипотез).
Для иллюстрации разных интерпретаций можно использовать графики функции мощности (критерия) для каждой проверки. Функция мощности дополняет функцию оперативной характеристики. В Natrella (J-1) и Bowkker and Lieberman (J-2) приводятся кривые оперативных характеристик для многих обычных (стандартных) статистических проверок. Мы будем вычислять схожую функции мощности для проверок из разделов 4.2.1 и 4.2.2. При выполнении этих проверках предполагается, что при проверке нулевой гипотезы CVt известен без погрешности, (и) что истинное среднее значение равно ПДК. Таким образом, значение 1.645*CVt* √(n) является мерой погрешности отбора проб и метода их анализа (у измеренного среднего значения стандартизованной концентрации).
Точнее - в этой формуле 1.645 является 95% перцентилью стандартизованного нормального распределения. Для получения верхнего одностороннего предела - 95%-го доверительного предела для истинной средней стандартизованной концентрации - вычисленное с помощью этой формулы значение добавляется к среднему измеренному значению (или же, для получения нижнего одностороннего предела, оно вычитается из среднего измеренного значения) в соответствии с разделами 4.2.1 и 4.2.2. (Для обсуждения значения используемого термина "уровень доверия" обратитесь к (cтатистическим замечаниям в 4.2.1.).
Если учитывать, что имеется погрешность как при определении среднего значения стандартизованного воздействия ẍ, так и при определении Cvt, то можно вычислить более точное значение 95% предела погрешности. (значения CVt, приведённые в техническом приложении D для методов отбора проб и их анализа NIOSH, были получены для 6 замеров для каждой из трёх концентраций загрязнений). Если это сделать, то коэффициент 1.645 для большинства из методов нужно будет увеличить примерно на 10%, чтобы учесть неопределённость экспериментально полученных значений CVt.
Но точный множитель, который нужно умножить на коэффициент 1.645 пока ещё нельзя вычислить, так как наши CVt определены при проведении измерений при тщательно контролируемом расходе воздуха при использовании критического отверстия. Значения CV для дополнительной погрешности (в производственных условиях) вызванные использованием индивидуального пробоотборного насоса (обозначаются CVр) были добавлены для получения консервативных значений CVt в техническом приложении D.
Мы используем CVt как известную величину[3], и используем нормальное распределение (а не Student-t) как основу для проверки статистики и для соответствующих функций мощности, приводимых ниже. Мы считаем, что при внесении (дополнительных) поправок с использованием результатов экспериментальных измерений CVp вместо 0.05, общий эффект такого уточнения пренебрежимо мал, поскольку ожидается, что две поправки дают вклад в противоположных направлениях.
Значение коэффициента 1.645 немного возрастёт, но оценка CVp (это компонент CVt), как ожидается, будет меньше, чем 0.05. В целом, мы считаем, что статистические проверки, описанные в разделах 4.2.1 и 4.2.2, а также графики функции мощности, приведённые в этом разделе - достаточно точные. Но - до тех пор, пока не будут получены более точные экспериментальные оценки погрешности пробоотборного насоса, - "половину ширины" доверительного интервала можно увеличить на примерно 10% (то есть - использовать 1.81 вместо 1.645).

Фиг. J-2. График функции мощности (критерия) для одностороннего интервала (при проверке работодателем и 5% уровне риска) для проверки выполнения требований законодательства согласно указаниям разделов 4.2.1 и 4.2.2. Вычисления проводились для коэффициента
Ниже приводится обсуждение вычисления кривых мощности. На Фиг. J-2 (графики приводятся) для проверки работодателем выполнения требований; статистическая проверка (согласно раздела 4.2.2.1) - верхний доверительный предел (95%):
UCL(95%) = ẍ+ [ 1/645*CVt ] / √(n)
где 1.645 является коэффициентом для одностороннего 95% предела у нормального распределения.
Если верхний доверительный предел UCL меньше 1, то результатом проведённой проверки является отбрасывание нулевой гипотезы Но о нарушении требований законодательства, и принятие альтернативной гипотезы На. Эквивалентным правилом для принятия решения является:
{ ẍ } < { 1 - [1.645*Cvt]/ √(n) } для выполнения требований законодательства.
Пример:
Для одиночного 8-часового замера (n=1) и CVt = 0.10 для выполнения требований необходимо, чтобы выполнялось условие:
{ ẍ } < { 0.8355 }
Для (получения) графика функции мощности (критерия) мы должны рассмотреть все возможные стандартизованные значения измеренных средних стандартизованных значений ẍ, которые могут быть получены, и те из них, которые могут привести к отбрасыванию нулевой гипотезы. Пусть истинное среднее стандартизованное воздействие μ/STD равно 0.9, то есть - что воздействие на рабочего меньше ПДК с запасом 10%. Когда мы проверяем нулевую гипотезу о нарушении требований законодательства, мощностью проверки будет вероятность того, что проверка результатов покажет выполнение требований, то есть - отвергнет нулевую гипотезу. Вероятность отбрасывания Но равна:
Вероятность [ ẍ < 0.8355 ]
Мы вычисляем стандартную нормальную переменную:
z = { 0.8355 - 0.9} / { CVt / √(n) } = -0.0645 / [ 0.10 / √(1) ] = -0.645
Вероятность отвергнуть Но - это вероятность получить значение, меньшее чем (-0.645) с помощью стандартного нормального распределения (среднее значение равно 0, изменчивость 1).
Вероятность { z < (-0.645) } ≈ 0.26
При таком подходе стандартизованное нормальное распределение было использовано для вычисления графиков, показанных на Фиг. J-2 ÷ J-6. Для вычислений использовали калькулятор Wang 2200 и программу PS.01-2200.01A-00f1-16-0 для вычисления интегралов нормального распределения.

Фиг. J-3. График функции мощности (критерия) для одностороннего интервала (при проверке инспектором и 5% уровне риска) для проверки нарушения требований законодательства согласно указаниям разделов 4.2.1 и 4.2.2. Вычисления проводились для коэффициента изменчивости отбора проб и их анализа CVt = 0.10 (погрешность около ± 20% при уровне доверия 95%).
Сравнение функций мощности для проверок,проводимых инспектором,
при уровнях значимости 1% и 5%
Для инспектора графики функции мощности (критерия) дают мощность (вероятность) того, что результаты измерений показывают нарушение требований, когда такое нарушение действительно существует. На Фиг. J-3 приводится график для проверки, проводимой инспектором, при уровне значимости (риске) 5%. Критерий (в этом случае) - повестка в суд не должна оформляться, если нижний 95% односторонний доверительный предел (95% LCL) значения воздействия на рабочего не превысил ПДК.
Так как вероятность ошибки первого рода 5%, может ли работодатель заявить,что его некорректно обвиняют в течение 5% времени? Конечно нет. Только в том случае, если истинное среднее воздействие на рабочего, у которого проводились измерения, немножко меньше ПДК, имеется вероятность 5% того, что будет ошибочно оформлена повестка в суд, и эта (вероятность) быстро снижается почти до нуля при истинных значениях воздействия на рабочих, меньших ПДК. Термин "5%-й уровень риска" относится к максимальному риску заявить о нарушении требований законодательства в случае, когда истинное среднее воздействие на рабочего почти равно ПДК.



Полезная информация: