Техническое приложение K
Статистическая теория (принятия) решений при измерении воздействий и ограничении кратковременных воздействий
При проведении измерений загрязнённости воздуха для определения того, не была ли концентрация загрязнений выше ПДК (кратковременной ПДК, обычно установленной для интервала 15 минут), проблема заключается в том, что на основании результатов, проводившихся в течение одного дня (нужно) сделать заключение о том, было ли превышение как в течение интервалов проведения измерений, так и в течение остальных интервалов времени (когда измерения не проводились) в этот день.
Принятие решения о степени воздействия в течение тех интервалов времени, когда проводились измерения
Для принятия решения о величине воздействия во время интервалов, когда проводились измерения, используется односторонний доверительный интервал для наибольшего измеренного воздействия. При определении этой величины предполагается, что случайные погрешности измерения соответствуют нормальному закону распределения, а стандартное отклонение известно.
Это стандартное отклонение определяется на основе коэффициента изменчивости способа отбора проб и их анализа. Если результаты всех сделанных измерений (с высокой степенью доверия) показывают, что в течение интервалов проведения замеров воздействие не превышало кратковременного ПДК, то для получения статистически-обоснованного вывода о воздействии в течение тех интервалов времени, когда измерения не проводились, используйте описанные ниже процедуры.
Оценка воздействия в течение тех интервалов времени,
когда измерения не проводились
Эту проблему можно сформулировать как проверку нулевой гипотезы:
Но: во всех случаях потенциальное воздействие было ниже кратковременного ПДК.
Альтернативная гипотеза: по крайней мере в одном случае потенциальное воздействие могло превысить кратковременную ПДК.
Предположим, что имеется результат ряда измерений кратковременных воздействий, (Xj, j=1… n) проводившихся в течение одного дня, и каждое из измерений проводилось в течение интервала времени, равного периоду, для которого установлено кратковременная ПДК. Пусть
xj = Xj / (кратковременная ПДК = CSTD). То есть - стандартизируем результаты измерений.
Эти измерения - кратковременны по продолжительности, и если они не проводились так, что "примыкали" друг к другу, то предполагается, что они - независимы, и одинаково распределены в соответствии с законом нормального распределения. Так как в нашем случае рассматривается только измерение с течением времени, то можно пренебречь случайной погрешностью отбора проб и их анализа.
При формулировании статистической модели используются десятичные логарифмы стандартизованных результатов измерений. Пусть
yi = Log[xj, j=1...n] (K-1)
Чтобы принять решение (о величине) кратковременного воздействия на рабочего, нужно проверить следующие гипотезы с (заданной) максимальной вероятностью допустить ошибки первого и второго рода.
Но: yi ≤ 0 для всех i = n+1, … N. (К-2)
Альтернативная гипотеза Н1: yi > 0 для хотя бы одного из i = n+1, … N. (К-3),
где N - число потенциально возможных замеров. Если кратковременная ПДК установлена для интервалов времени 15 минут, то (для 8-часовой смены) N = 32. Но - это гипотеза, которая справедлива при воздействии, меньшем ПДК, то есть - при выполнении требований законодательства. А Н1 - это альтернативная гипотеза о нарушении требований законодательства. Если ни один из этих двух выводов не может быть сделан с достаточно большим уровнем доверия, то такой случай рассматривают как возможное чрезмерное воздействие.
Описанная выше проблема проверки гипотез может быть сформулирована с помощью терминологии, использующей вероятность. Для данного ряда результатов измерений yn Δ {y1, … yn} вычислим вероятность выполнения требований законодательства Рс:
Pc Δ {yn+1 ≤ 0, ...yN ≤ 0│yn} (K-4)
Плотность вероятности для одного из потенциальных замеров можно записать как
p(yk│yn) = p[yk,μ,σ] * dμ * dσ, k=n+1 … N (K-5)
где μ и σ - неизвестные величины (среднее значение и стандартное отклонения) результатов измерений yj для j=1, … N, а р(yj,μ,σ│yn ) - это объединение пост-априорной плотности yj, μ и σ для полученных результатов yn. Используя (основанное на вере/фидуцированное) распределение μ (см. ссылку К-1)
μ ~ N ( ӯ ; σ2 / n) (K-6)
где N(a,b) - нормальная плотность со средним значением a и изменчивостью b, и
(среднее значение) ӯ = (1/n)*[Σyi, i=1, … n] (K-7)
Предположив, что имеющееся σ известно, тогда с помощью уравнения К-5 получим
p(yk│yn) = N { ӯ ; σ2 (1+1/n)} (K-8)
Затем
P{yk>0│yn} = 0∞N [yk; ӯ, σ2 * (1+1/n)] dyk Δ β для k = n=1 … N (K-9)
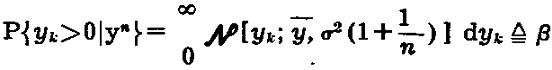
Теперь вероятность выполнения требований Рс равна
Pc = П{ P(yk≤0) } (для всех k = n=1 … N) = П[ 1 - { P(yk>0) }] (для всех k = n=1 … N) (К-10)
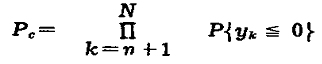
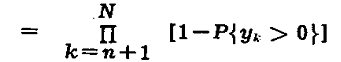
Используя замечание, сделанное для уравнения (К-9) получим:
Pc = (1-β)N-n (K-11)
Если (N-n)β <<1, то достаточно точный результат можно получить с помощью приближённой формулы
Pc = 1- (N-n)β (K-12)
Предположение о известности σ не вполне оправдано. Учитывать эту дополнительную неопределённость для (К-2) можно с помощью Байесовских аргументов с диффузными изменениями (Bayesian arguments with diffuse priors). Но полученная процедура получается настолько сложной, что её трудно выполнить. Для уравнения (К-9) рекомендуется использовать вместо σ2 - изменчивость s2 :
s2 = 1/(n-1) * { Σ [yj- ӯ ]2 для всех j=1...n} (K-13)
для вычисления изменчивости результатов сделанных измерений.
Уравнение (К-11) показывает, что если N-n (число интервалов, когда измерения не проводились) велико, то вероятность (подтверждённого) выполнения требований законодательства становится маленькой. А вероятность того, что хотя бы в одном случае произошло превышение ПДК - возрастает. Поэтому прямое применение уравнения (К-11) может дать чрезмерно пессимистический результат.
Это привело к (использованию) теории ожидаемого числа "пиков" в течение дня. Предположим, что для выполнения нескольких случайных измерений во время ожидаемо-критических интервалов времени использовался способ измерений, не лишённый погрешности. Если известен характер технологического процесса, можно определить общее число таких потенциально опасных интервалов в течение дня для уравнения (К-9) - ( ṅ ), а не ( N-n ).
Если в течение всех ṅ интервалов проводились замеры, то приведённая процедура (принятия решений для интервалов, когда измерения не проводились) становится ненужной - требуется только проверить выполнение условий, описанных в разделе (Оценка воздействия в течение тех интервалов времени, когда измерения не проводились) выше. Повторим причины разработки метода оценки для проведения измерений в течение не всех потенциально опасных интервалов: уменьшение нагрузки на работодателя. Таким образом, если сделанные замеры проводились в течение потенциально опасных интервалов (но не всех), и имеется ещё ń дополнительных потенциально опасных интервалов, когда измерения не проводились, то классификацию воздействия проводят на основе
Pc = (1-β)*ṅ (K-14)
- если уже сделанные замеры не показали, что было превышение ПДК. Если вероятность выполнения требований законодательства Рс превышает (принятое сейчас) пороговое значение - скажем, 0.9 - то считается, что рабочий не подвергался чрезмерному воздействию. С другой стороны, если Рс меньше другого порогового значения, скажем - 0.1, то можно считать, что рабочий подвергался чрезмерному воздействию. Если же вероятность приняла какое-то промежуточное значение, то считается, что рабочий потенциально подвергается чрезмерному воздействию.
Ссылки
K-1. Kendall MS and A Stuart: The Advanced Theory of Statistics. Hafner Publishing Co., New York, NY, Volume I, 1969, and Volume II, 1967.
K-2. Bar-Shalom Y, D Budenaers, R Schainker and Segall: Handbook of Statistical Tests for Evaluating Employee Exposure to Air Contaminants. NIOSH Technical Information, Pub. No. (NIOSH) 75-147, Cincinnati, Ohio 45226, April 1975.



Полезная информация:
Статистическая теория (принятия) решений при измерении воздействий и ограничении кратковременных воздействий
При проведении измерений загрязнённости воздуха для определения того, не была ли концентрация загрязнений выше ПДК (кратковременной ПДК, обычно установленной для интервала 15 минут), проблема заключается в том, что на основании результатов, проводившихся в течение одного дня (нужно) сделать заключение о том, было ли превышение как в течение интервалов проведения измерений, так и в течение остальных интервалов времени (когда измерения не проводились) в этот день.
Принятие решения о степени воздействия в течение тех интервалов времени, когда проводились измерения
Для принятия решения о величине воздействия во время интервалов, когда проводились измерения, используется односторонний доверительный интервал для наибольшего измеренного воздействия. При определении этой величины предполагается, что случайные погрешности измерения соответствуют нормальному закону распределения, а стандартное отклонение известно.
Это стандартное отклонение определяется на основе коэффициента изменчивости способа отбора проб и их анализа. Если результаты всех сделанных измерений (с высокой степенью доверия) показывают, что в течение интервалов проведения замеров воздействие не превышало кратковременного ПДК, то для получения статистически-обоснованного вывода о воздействии в течение тех интервалов времени, когда измерения не проводились, используйте описанные ниже процедуры.
Оценка воздействия в течение тех интервалов времени,
когда измерения не проводились
Эту проблему можно сформулировать как проверку нулевой гипотезы:
Но: во всех случаях потенциальное воздействие было ниже кратковременного ПДК.
Альтернативная гипотеза: по крайней мере в одном случае потенциальное воздействие могло превысить кратковременную ПДК.
Предположим, что имеется результат ряда измерений кратковременных воздействий, (Xj, j=1… n) проводившихся в течение одного дня, и каждое из измерений проводилось в течение интервала времени, равного периоду, для которого установлено кратковременная ПДК. Пусть
xj = Xj / (кратковременная ПДК = CSTD). То есть - стандартизируем результаты измерений.
Эти измерения - кратковременны по продолжительности, и если они не проводились так, что "примыкали" друг к другу, то предполагается, что они - независимы, и одинаково распределены в соответствии с законом нормального распределения. Так как в нашем случае рассматривается только измерение с течением времени, то можно пренебречь случайной погрешностью отбора проб и их анализа.
При формулировании статистической модели используются десятичные логарифмы стандартизованных результатов измерений. Пусть
yi = Log[xj, j=1...n] (K-1)
Чтобы принять решение (о величине) кратковременного воздействия на рабочего, нужно проверить следующие гипотезы с (заданной) максимальной вероятностью допустить ошибки первого и второго рода.
Но: yi ≤ 0 для всех i = n+1, … N. (К-2)
Альтернативная гипотеза Н1: yi > 0 для хотя бы одного из i = n+1, … N. (К-3),
где N - число потенциально возможных замеров. Если кратковременная ПДК установлена для интервалов времени 15 минут, то (для 8-часовой смены) N = 32. Но - это гипотеза, которая справедлива при воздействии, меньшем ПДК, то есть - при выполнении требований законодательства. А Н1 - это альтернативная гипотеза о нарушении требований законодательства. Если ни один из этих двух выводов не может быть сделан с достаточно большим уровнем доверия, то такой случай рассматривают как возможное чрезмерное воздействие.
Описанная выше проблема проверки гипотез может быть сформулирована с помощью терминологии, использующей вероятность. Для данного ряда результатов измерений yn Δ {y1, … yn} вычислим вероятность выполнения требований законодательства Рс:
Pc Δ {yn+1 ≤ 0, ...yN ≤ 0│yn} (K-4)
Плотность вероятности для одного из потенциальных замеров можно записать как
p(yk│yn) = p[yk,μ,σ] * dμ * dσ, k=n+1 … N (K-5)
где μ и σ - неизвестные величины (среднее значение и стандартное отклонения) результатов измерений yj для j=1, … N, а р(yj,μ,σ│yn ) - это объединение пост-априорной плотности yj, μ и σ для полученных результатов yn. Используя (основанное на вере/фидуцированное) распределение μ (см. ссылку К-1)
μ ~ N ( ӯ ; σ2 / n) (K-6)
где N(a,b) - нормальная плотность со средним значением a и изменчивостью b, и
(среднее значение) ӯ = (1/n)*[Σyi, i=1, … n] (K-7)
Предположив, что имеющееся σ известно, тогда с помощью уравнения К-5 получим
p(yk│yn) = N { ӯ ; σ2 (1+1/n)} (K-8)
Затем
P{yk>0│yn} = 0∞N [yk; ӯ, σ2 * (1+1/n)] dyk Δ β для k = n=1 … N (K-9)
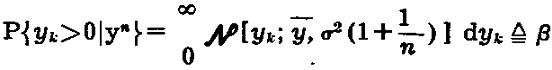
Теперь вероятность выполнения требований Рс равна
Pc = П{ P(yk≤0) } (для всех k = n=1 … N) = П[ 1 - { P(yk>0) }] (для всех k = n=1 … N) (К-10)
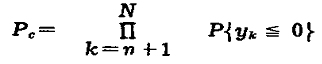
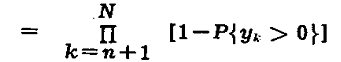
Используя замечание, сделанное для уравнения (К-9) получим:
Pc = (1-β)N-n (K-11)
Если (N-n)β <<1, то достаточно точный результат можно получить с помощью приближённой формулы
Pc = 1- (N-n)β (K-12)
Предположение о известности σ не вполне оправдано. Учитывать эту дополнительную неопределённость для (К-2) можно с помощью Байесовских аргументов с диффузными изменениями (Bayesian arguments with diffuse priors). Но полученная процедура получается настолько сложной, что её трудно выполнить. Для уравнения (К-9) рекомендуется использовать вместо σ2 - изменчивость s2 :
s2 = 1/(n-1) * { Σ [yj- ӯ ]2 для всех j=1...n} (K-13)
для вычисления изменчивости результатов сделанных измерений.
Уравнение (К-11) показывает, что если N-n (число интервалов, когда измерения не проводились) велико, то вероятность (подтверждённого) выполнения требований законодательства становится маленькой. А вероятность того, что хотя бы в одном случае произошло превышение ПДК - возрастает. Поэтому прямое применение уравнения (К-11) может дать чрезмерно пессимистический результат.
Это привело к (использованию) теории ожидаемого числа "пиков" в течение дня. Предположим, что для выполнения нескольких случайных измерений во время ожидаемо-критических интервалов времени использовался способ измерений, не лишённый погрешности. Если известен характер технологического процесса, можно определить общее число таких потенциально опасных интервалов в течение дня для уравнения (К-9) - ( ṅ ), а не ( N-n ).
Если в течение всех ṅ интервалов проводились замеры, то приведённая процедура (принятия решений для интервалов, когда измерения не проводились) становится ненужной - требуется только проверить выполнение условий, описанных в разделе (Оценка воздействия в течение тех интервалов времени, когда измерения не проводились) выше. Повторим причины разработки метода оценки для проведения измерений в течение не всех потенциально опасных интервалов: уменьшение нагрузки на работодателя. Таким образом, если сделанные замеры проводились в течение потенциально опасных интервалов (но не всех), и имеется ещё ń дополнительных потенциально опасных интервалов, когда измерения не проводились, то классификацию воздействия проводят на основе
Pc = (1-β)*ṅ (K-14)
- если уже сделанные замеры не показали, что было превышение ПДК. Если вероятность выполнения требований законодательства Рс превышает (принятое сейчас) пороговое значение - скажем, 0.9 - то считается, что рабочий не подвергался чрезмерному воздействию. С другой стороны, если Рс меньше другого порогового значения, скажем - 0.1, то можно считать, что рабочий подвергался чрезмерному воздействию. Если же вероятность приняла какое-то промежуточное значение, то считается, что рабочий потенциально подвергается чрезмерному воздействию.
Ссылки
K-1. Kendall MS and A Stuart: The Advanced Theory of Statistics. Hafner Publishing Co., New York, NY, Volume I, 1969, and Volume II, 1967.
K-2. Bar-Shalom Y, D Budenaers, R Schainker and Segall: Handbook of Statistical Tests for Evaluating Employee Exposure to Air Contaminants. NIOSH Technical Information, Pub. No. (NIOSH) 75-147, Cincinnati, Ohio 45226, April 1975.



Полезная информация: