Техническое приложение M
Нормальное и логарифмически-нормальное распределение частот
Статистические методы, обсуждаемые в этом разделе предполагают, что концентрации воздушных загрязнений, которые измерялись в производственных условиях случайным образом, являются независимыми, и что они соответствуют логарифмически-нормальному закону распределения - и в течение одной конкретной смены, и среднесменные значения (измеренные в разные дни).
Кроме того, предполагается, что при отборе проб и проведении их анализа погрешности измерений независимы, и соответствуют нормальному закону распределения. Ниже приводится объяснение того, почему эти виды распределения были выбраны для моделирования распределения результатов измерений. Эти причины достаточно просты. Их выбрали потому, что при проведении измерений в промышленной гигиене они встречаются очень часто, потому что (эти распределения) простые, и потому, что их свойства хорошо изучены. (Но) эмпирические наблюдения, показывающие что результаты измерений хорошо соответствуют математическим моделям, использующим нормальное и логарифмически-нормальное распределения, не гарантируют, что результаты всех измерений соответствуют этим моделям.
Если имеются какие-то сомнения относительно того, что использование нормального или логарифмически-нормального распределения приемлемо, то первым шагом при анализе результатов должно стать построение диаграммы распределения или графика в системе координат (логарифмически-вероятностной), описанной в техническом приложении I. Также посмотрите это приложение (I) с примерами результатов, которые могут плохо описываться логарифмически-нормальным распределением.
Прежде чем анализировать статистические сведения, нам нужно определить распределение частот результатов, или же сделать какие-то предположения. Roach (M-2 - M-4) и Kerr (M-5) предположили, что результаты измерений параметров окружающей среды соответствуют закону нормального распределения. Но хорошо известно, что в большинстве случаев распределение значений загрязнённости воздуха населённых мест лучше описывается логарифмически-нормальным распределением (с использованием натуральных или десятичных логарифмов).
Таким образом, логарифмы результатов измерений соответствуют нормальному распределению. Важно, что Breslin et al (M-10), Sherwood (V-11, M-12), Jones and Brief (M-13), Gale (M-14, M-15), Coenen (M-16, M-17), Hounam (M-18) и Juda and Budzinski (M-19, M-20) показали, что результаты измерения производственных воздействий, и при замерах в закрытых помещениях, и на открытом воздухе, и для коротких периодов времени (секунды), и для больших интервалов (дни) - соответствуют логарифмически-нормальному распределению.
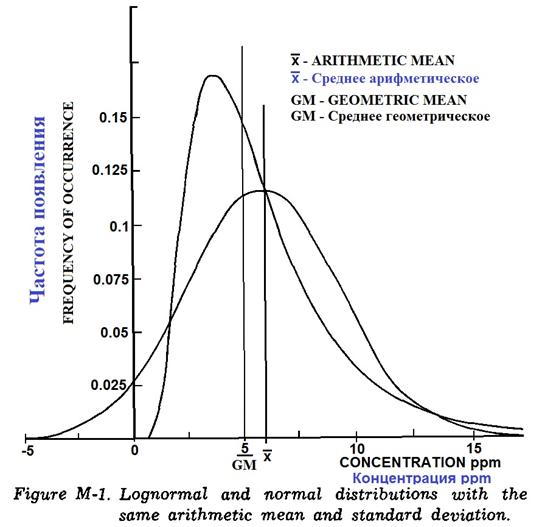
Каково отличие между результатами измерений, соответствующими нормальному и логарифмически-нормальному распределениям? Во-первых, нужно помнить, что нормальное распределение полностью определяется средним арифметическим μ и стандартным отклонением σ. А логарифмически-нормальное распределение полностью определяется медианой, или средним геометрическим (GM), и стандартным геометрическим отклонением (GSD). Если исходные значения соответствуют логарифмически-нормальному распределению, то их логарифмическое преобразование даёт результат - данные, соответствующие нормальному распределению.
GM и GSD логарифмически-нормального распределения - это антилогарифмы среднего значения и стандартного отклонения после их логарифмического преобразования. У нормального распределения - симметричная форма графика, а при логарифмически-нормальном распределении график обычно положительно скошен (длинный "хвост" справа показывает, что по сравнению с нормальным распределением вероятность того, что будет большая концентрация - выше). На Фиг. М-1 сравниваются нормальное и логарифмически-нормальное распределения, у которых одинаковые μ и σ. При проведении измерений в промышленной гигиене (М-16) обнаружилось, что условия, способствующими появлению логарифмически - нормального распределения, являются (но это - необязательно):
- Концентрации охватывают широкий диапазон значений, иногда - изменяясь на несколько порядков.
- Концентрации близки к физическому пределу (нулевые концентрации).
- Изменчивость измеренных концентраций - того же порядка, что и сами концентрации.
- Существует конечная (не нулевая) вероятность того, что будут очень большие концентрации ("пики").
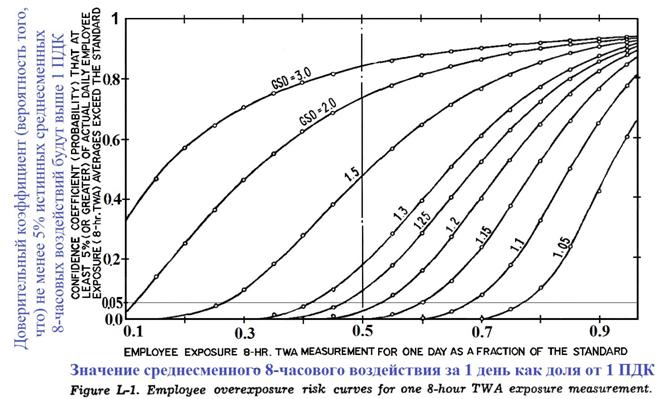
Фиг. М-1. Графики нормального и логарифмически-нормального распределений, у которых одинаковые средние арифметические значения и стандартные отклонения
Изменчивость результатов измерений в производственных условиях (то есть, отличие между результатами повторных измерений на одном и том же месте) обычно можно разделить на три составляющие: случайные погрешности метода отбора проб, случайные погрешности метода их анализа, и изменчивость концентрации с течением времени. Два первых компонента изменчивости обычно известны заранее, и они примерно соответствуют закону нормального распределения. А вот изменения концентрации воздушных загрязнений на предприятии обычно превышают (диапазон измерения) известного измерительного оборудования (часто - в 10-20раз). В статье LeClare et al (M-21) обсуждаются эти компоненты.
Когда для оценки средней концентрации воздушных загрязнений на предприятии и определения среднего воздействия на рабочего делается несколько измерений, следует предполагать, что значения соответствуют логарифмически-нормальному распределению. Но в особых условиях следует предполагать, что распределение нормальное, например - если проводятся измерения для определения того, не превышена ли кратковременная ПДК, и если замер(ы) проводятся в течение всего интервала времени, для которого определена ПДК. В этих случаях, весь интересующий интервал охватывается временем проведения измерений, и на результат влияет только погрешность отбора проб и их анализа, которые соответствуют нормальному распределению.
Относительная изменчивость нормального распределения (как например - случайные погрешности измерения и анализа) обычно (описывают) коэффициентом изменчивости (CV). Коэффициент изменчивости CV также известен как относительное стандартное отклонение. CV - это полезный показатель "рассеивания". Истинное значение среднего воздействия, плюс/минус два CV, охватывает около 95% от результатов измерений. Таким образом, если для повторных измерений какого-то не изменяющегося физического параметра используется способ измерений с CV = 10% (например - концентрация химического вещества в мензурке в растворе), то около 95% от результатов измерений будет находится в пределах ±20% (2 * CV) от истинного среднего значения.
К сожалению, свойства, которые мы пытаемся измерить - концентрация вредных веществ, воздействующих на рабочих - не постоянна. Во-первых, она изменяется в течение 8-часового измерения среднесменного воздействия. При проведении серии кратковременных измерений в зоне дыхания (длительность одного замера обычно меньше 30 минут) такая изменчивость обычно выявляется - результаты этих измерений обычно очень непостоянны. Но эта изменчивость можно устранить, если проводить замеры в течение всей смены, как обсуждали в (M-1) Leidel and Bush. Во-вторых, распределение значений среднесменных воздействий, измеренных в разные дни, также соответствует логарифмически-нормальному распределению.
Для описания непостоянства внешних условий используют GSD. Если GSD = 1, то это означает, что внешние условия абсолютно постоянны. GSD = 2.0 и больше соответствуют очень непостоянным внешним условиям. Hald (M-22) заявил, что форма графика при логарифмически-нормальном распределении, и при маленькой изменчивости (например, при GSD< ~1/4) примерно соответствует форме кривой нормального распределения. Для этих GSD существует примерное соответствие между CV и GSD-1:
GSD
(GSD - 1)
СV
1.05
0.05
0.049
1.10
0.10
0.096
1.20
0.20
0.018
1.30
0.30
0.027
1.40
0.40
0.035
Для тех, кто хочет узнать о логнормальном распределении больше, рекомендуется Aitchinson and Brown (M-23).На Фиг. М-2 показаны различные логнормальные распределения, у которых одинаково среднее арифметическое значение - 10 ppm. Показаны графики для GSD = 1.2б 1.5б 2.0 и 3.0.
Фиг. М-2. (Разные) логарифмически-нормальные распределения концентрации при одинаковом среднем арифметическом значении 10 ppm
Формулы преобразования для логарифмически-нормалльного распределения
Если значения переменной (Ln X) соответствуют нормальному распределению (а значения Х- логарифмически-нормальному распределению), то мы можем определить:
μ - истинное среднее арифметическое распределения значений (Х),
σ - истинное стандартное отклонение распределения значений (Х).
μl - истинное среднее арифметическое распределения значений (Ln Х),
σl - истинное стандартное отклонение распределения значений значений (Ln Х).
GM - среднее геометрическое распределения значений (Х).
GSD - стандартное геометрическое отклонение = exp[σl], когда для вычисления σl используется (Ln Х).
GSD = antilog10[σl], когда используется (Log10 X). В таблице М-1 показаны взаимосвязи между этими шестью параметрами.
Замечания:
1. Эти взаимосвязи применимы только в отношении истинных параметров исходного распределения. Их нельзя использовать для параметров, полученных при проведении измерений, за исключением случаев проведения грубой, неточной и приближённой оценки.
2. GM и GSD используются для описания параметров или исходного (истинного) распределения, или полученных при проведении измерений. Но их нельзя использовать в описанных ниже уравнениях взаимосвязей, если они не получены путём вычислений на основе истинного распределения.
3. Вне зависимости от того,какие логарифмы используются (натуральные или десятичные) для вычисления σl, значение GSD не изменяется
Таблица M-1. Взаимосвязи между логарифмическими параметрами и арифметическими параметрами логарифмически-нормального распределения
Дано
Чтобы получить:
Используйте (формулу):
μl
μ, σ
GM =
GM =
exp(μl)
μ2 / √(μ2+σ2)
σl
μ, σ
GSD =
GSD =
exp (σl)
exp( √[ln{1 + σ2/μ2}])
μl, σl
GM, σl
μ =
μ =
exp{μl+ 0.5*σl2}
(GM)exp{0.5*σl2}
μl, σl
GM, σl
σ =
σ =
√{ [2*μl+σl2]*[exp(σl2) - 1]}
√{ (GM)2*[exp(σl2)]*[exp(σl2) - 1]}
GM
μl, σl
μl =
μl =
Ln{GM}
Ln{μ} - 0.5*σl2
GSD
μ, σ
σl =
σl =
Ln{GSD}
√{ Ln[1+σ2/μ2]}
μl, σl
Мода
exp(μl - σl2) = самое часто встречающееся значение
Ссылки
М-1. Leidel and KA Busch: Statistical Methods for the Determination of Non-compliance with Occupational Health Standards. NIOSH Technical Information, HEW Pub. No. 75-159, Cincinnati, Ohio.
М-2. Roach RA: Testing Compliance with ACGIH Threshold Limit Values for Respirable Dusts Evaluated by Count. Transactions of the American Industrial Hygiene Association, pp. 27-39, 1966.
М-3. Roach SA: A More Rational Basis for Air Sampling Programs. American Industrial Hygiene Association Journal 27:1-12, 1966.
М-4. Roach SA, EJ Baier, HE Ayer and RL Harris: Testing Compliance with Threshold Limit Values for Respirable Dusts. American Industrial Hygiene Association Journal 28:543-553, 1967.
М-5. Kerr GW: Use of Statistical Methodology in Environmental Monitoring. American Industrial Hygiene Association Journal 23:75-82, 1962.
М-6. Larsen RI: A Method for Determining Source Reduction Required to Meet Quality Standards. Journal of Air Pollution Control Association 11:71, 1961.
М-7. Larsen RI: A New Mathematical Model of Air Pollutant Concentration Averaging Time and Frequency. Journal of Air Pollution Control Association 19:24, 1969.
М-8. Phinney DE and JE Newman: The Precision Associated with the Sampling Frequencies of Total Particulate at Indianapolis, Indiana. Journal of the Air Pollution Control Association, 22:692-695, 1972.
М-9. Larsen RI: A Mathematical Model for Relating Air Quality Measurements to Air Quality Standards. US Environmental Protection Agency. AP-89, 1971.
М-10. Breslin AJ, Ong L, H Glauberman, AC Gejrge and P LeClare: The Accuracy of Dust Exposure Estimates Obtained from Conventional Air Sampling. American Industrial Hygiene Association Journal 28:56-61, 1967.
М-11. Sherwood RJ: On the Interpretation of Air Sampling for Radioactive Particles. American Industrial Hygiene Association Journal 27:98-109, 1966.
М-12. Sherwood RJ: The monitoring of Benzene Ehposure by Air Sampling. American Industrial Hygiene Association Journal 32:840-846, 1971.
М-13. Jones AR and Brief: Evaluating Benzene Exposures. American Industrial Hygiene Association Journal. 32:610-613, 1971.
М-14. Gale HJ: The Lognormal Distribution and Some Examples of Its Application in the Field of Radiation Protection. Atomic Energy Research Establishment Report AERE-R 4736, Her Majesty’s Stationery Office, London, England, 1965.
М-15. Gale HJ. Some Examples of the Application of the Lognormal Distribution in Radiation Protection. Annals of Occupational Hygiene, 10:39-45, 1967.
М-16. Coenen W: The Confidence Limits for the Mean Values of Dust Concentration. Staub (English Translation), 26:39-45, May 1966.
М-17. Coenen W: Measurement Assessment of the Concentration of Health Impairing, Especially Silicogenic Dusts at Work Places of Surface Industries. Staub (English Translation), 31:16-23, December 1971.
М-18. Hounam RF: An Application of the Log-Normal Distribution to Some Air Sampling Results and Recommendations on the Interpretation of Air Sampling Data. Atomic Energy Research Establishment Report AERE-M 1469. Her Majesty’s Stationery Office, London, England, 1965.
М-19. Juda J and K Budzinski: Feher bei der Bestimmiung der mittleren Staub-konzentration als Funktion der Anzahl der Einzelmessugen (Errors in Determinating the Mean Dust Concentration as a Function of the Number of Individual Measurements). Staub, 24:283-287 (English translation), Augest 1987.
M-20. Juda J and K Budzinski: Determining the Tolerance Range of the Mean Value of Dust Concentration, Staub, 27:12-16 (English translation), April 1987.
М-21. LeCare PL, AJ Breslin and L Ong: Factors Affecting the Accuracy of Average Dust Concentration Measurements. American Industrial Hygiene Association Journal 30:386-393, 1969.
М-22. Hald A: Statistical Theory with Engineering Applications. John Wiley and Sons, New York, NY 1952.
М-23. Aitchinson J and JAC Brown: The Lognormal Distribution. Cambridge University Press, Cambridge, England 1963.



Полезная информация:
Нормальное и логарифмически-нормальное распределение частот
Статистические методы, обсуждаемые в этом разделе предполагают, что концентрации воздушных загрязнений, которые измерялись в производственных условиях случайным образом, являются независимыми, и что они соответствуют логарифмически-нормальному закону распределения - и в течение одной конкретной смены, и среднесменные значения (измеренные в разные дни).
Кроме того, предполагается, что при отборе проб и проведении их анализа погрешности измерений независимы, и соответствуют нормальному закону распределения. Ниже приводится объяснение того, почему эти виды распределения были выбраны для моделирования распределения результатов измерений. Эти причины достаточно просты. Их выбрали потому, что при проведении измерений в промышленной гигиене они встречаются очень часто, потому что (эти распределения) простые, и потому, что их свойства хорошо изучены. (Но) эмпирические наблюдения, показывающие что результаты измерений хорошо соответствуют математическим моделям, использующим нормальное и логарифмически-нормальное распределения, не гарантируют, что результаты всех измерений соответствуют этим моделям.
Если имеются какие-то сомнения относительно того, что использование нормального или логарифмически-нормального распределения приемлемо, то первым шагом при анализе результатов должно стать построение диаграммы распределения или графика в системе координат (логарифмически-вероятностной), описанной в техническом приложении I. Также посмотрите это приложение (I) с примерами результатов, которые могут плохо описываться логарифмически-нормальным распределением.
Прежде чем анализировать статистические сведения, нам нужно определить распределение частот результатов, или же сделать какие-то предположения. Roach (M-2 - M-4) и Kerr (M-5) предположили, что результаты измерений параметров окружающей среды соответствуют закону нормального распределения. Но хорошо известно, что в большинстве случаев распределение значений загрязнённости воздуха населённых мест лучше описывается логарифмически-нормальным распределением (с использованием натуральных или десятичных логарифмов).
Таким образом, логарифмы результатов измерений соответствуют нормальному распределению. Важно, что Breslin et al (M-10), Sherwood (V-11, M-12), Jones and Brief (M-13), Gale (M-14, M-15), Coenen (M-16, M-17), Hounam (M-18) и Juda and Budzinski (M-19, M-20) показали, что результаты измерения производственных воздействий, и при замерах в закрытых помещениях, и на открытом воздухе, и для коротких периодов времени (секунды), и для больших интервалов (дни) - соответствуют логарифмически-нормальному распределению.
Каково отличие между результатами измерений, соответствующими нормальному и логарифмически-нормальному распределениям? Во-первых, нужно помнить, что нормальное распределение полностью определяется средним арифметическим μ и стандартным отклонением σ. А логарифмически-нормальное распределение полностью определяется медианой, или средним геометрическим (GM), и стандартным геометрическим отклонением (GSD). Если исходные значения соответствуют логарифмически-нормальному распределению, то их логарифмическое преобразование даёт результат - данные, соответствующие нормальному распределению.
GM и GSD логарифмически-нормального распределения - это антилогарифмы среднего значения и стандартного отклонения после их логарифмического преобразования. У нормального распределения - симметричная форма графика, а при логарифмически-нормальном распределении график обычно положительно скошен (длинный "хвост" справа показывает, что по сравнению с нормальным распределением вероятность того, что будет большая концентрация - выше). На Фиг. М-1 сравниваются нормальное и логарифмически-нормальное распределения, у которых одинаковые μ и σ. При проведении измерений в промышленной гигиене (М-16) обнаружилось, что условия, способствующими появлению логарифмически - нормального распределения, являются (но это - необязательно):
- Концентрации охватывают широкий диапазон значений, иногда - изменяясь на несколько порядков.
- Концентрации близки к физическому пределу (нулевые концентрации).
- Изменчивость измеренных концентраций - того же порядка, что и сами концентрации.
- Существует конечная (не нулевая) вероятность того, что будут очень большие концентрации ("пики").

Фиг. М-1. Графики нормального и логарифмически-нормального распределений, у которых одинаковые средние арифметические значения и стандартные отклонения
Изменчивость результатов измерений в производственных условиях (то есть, отличие между результатами повторных измерений на одном и том же месте) обычно можно разделить на три составляющие: случайные погрешности метода отбора проб, случайные погрешности метода их анализа, и изменчивость концентрации с течением времени. Два первых компонента изменчивости обычно известны заранее, и они примерно соответствуют закону нормального распределения. А вот изменения концентрации воздушных загрязнений на предприятии обычно превышают (диапазон измерения) известного измерительного оборудования (часто - в 10-20раз). В статье LeClare et al (M-21) обсуждаются эти компоненты.
Когда для оценки средней концентрации воздушных загрязнений на предприятии и определения среднего воздействия на рабочего делается несколько измерений, следует предполагать, что значения соответствуют логарифмически-нормальному распределению. Но в особых условиях следует предполагать, что распределение нормальное, например - если проводятся измерения для определения того, не превышена ли кратковременная ПДК, и если замер(ы) проводятся в течение всего интервала времени, для которого определена ПДК. В этих случаях, весь интересующий интервал охватывается временем проведения измерений, и на результат влияет только погрешность отбора проб и их анализа, которые соответствуют нормальному распределению.
Относительная изменчивость нормального распределения (как например - случайные погрешности измерения и анализа) обычно (описывают) коэффициентом изменчивости (CV). Коэффициент изменчивости CV также известен как относительное стандартное отклонение. CV - это полезный показатель "рассеивания". Истинное значение среднего воздействия, плюс/минус два CV, охватывает около 95% от результатов измерений. Таким образом, если для повторных измерений какого-то не изменяющегося физического параметра используется способ измерений с CV = 10% (например - концентрация химического вещества в мензурке в растворе), то около 95% от результатов измерений будет находится в пределах ±20% (2 * CV) от истинного среднего значения.
К сожалению, свойства, которые мы пытаемся измерить - концентрация вредных веществ, воздействующих на рабочих - не постоянна. Во-первых, она изменяется в течение 8-часового измерения среднесменного воздействия. При проведении серии кратковременных измерений в зоне дыхания (длительность одного замера обычно меньше 30 минут) такая изменчивость обычно выявляется - результаты этих измерений обычно очень непостоянны. Но эта изменчивость можно устранить, если проводить замеры в течение всей смены, как обсуждали в (M-1) Leidel and Bush. Во-вторых, распределение значений среднесменных воздействий, измеренных в разные дни, также соответствует логарифмически-нормальному распределению.
Для описания непостоянства внешних условий используют GSD. Если GSD = 1, то это означает, что внешние условия абсолютно постоянны. GSD = 2.0 и больше соответствуют очень непостоянным внешним условиям. Hald (M-22) заявил, что форма графика при логарифмически-нормальном распределении, и при маленькой изменчивости (например, при GSD< ~1/4) примерно соответствует форме кривой нормального распределения. Для этих GSD существует примерное соответствие между CV и GSD-1:
|
GSD |
(GSD - 1) |
СV |
|
1.05 |
0.05 |
0.049 |
|
1.10 |
0.10 |
0.096 |
|
1.20 |
0.20 |
0.018 |
|
1.30 |
0.30 |
0.027 |
|
1.40 |
0.40 |
0.035 |
Для тех, кто хочет узнать о логнормальном распределении больше, рекомендуется Aitchinson and Brown (M-23).На Фиг. М-2 показаны различные логнормальные распределения, у которых одинаково среднее арифметическое значение - 10 ppm. Показаны графики для GSD = 1.2б 1.5б 2.0 и 3.0.

Фиг. М-2. (Разные) логарифмически-нормальные распределения концентрации при одинаковом среднем арифметическом значении 10 ppm
Формулы преобразования для логарифмически-нормалльного распределения
Если значения переменной (Ln X) соответствуют нормальному распределению (а значения Х- логарифмически-нормальному распределению), то мы можем определить:
μ - истинное среднее арифметическое распределения значений (Х),
σ - истинное стандартное отклонение распределения значений (Х).
μl - истинное среднее арифметическое распределения значений (Ln Х),
σl - истинное стандартное отклонение распределения значений значений (Ln Х).
GM - среднее геометрическое распределения значений (Х).
GSD - стандартное геометрическое отклонение = exp[σl], когда для вычисления σl используется (Ln Х).
GSD = antilog10[σl], когда используется (Log10 X). В таблице М-1 показаны взаимосвязи между этими шестью параметрами.
Замечания:
1. Эти взаимосвязи применимы только в отношении истинных параметров исходного распределения. Их нельзя использовать для параметров, полученных при проведении измерений, за исключением случаев проведения грубой, неточной и приближённой оценки.
2. GM и GSD используются для описания параметров или исходного (истинного) распределения, или полученных при проведении измерений. Но их нельзя использовать в описанных ниже уравнениях взаимосвязей, если они не получены путём вычислений на основе истинного распределения.
3. Вне зависимости от того,какие логарифмы используются (натуральные или десятичные) для вычисления σl, значение GSD не изменяется
Таблица M-1. Взаимосвязи между логарифмическими параметрами и арифметическими параметрами логарифмически-нормального распределения
|
Дано |
Чтобы получить: |
Используйте (формулу): |
|
μl μ, σ |
GM = GM = |
exp(μl) μ2 / √(μ2+σ2) |
|
σl μ, σ |
GSD = GSD = |
exp (σl) exp( √[ln{1 + σ2/μ2}]) |
|
μl, σl GM, σl |
μ = μ = |
exp{μl+ 0.5*σl2} (GM)exp{0.5*σl2} |
|
μl, σl GM, σl |
σ = σ = |
√{ [2*μl+σl2]*[exp(σl2) - 1]} √{ (GM)2*[exp(σl2)]*[exp(σl2) - 1]} |
|
GM μl, σl |
μl = μl = |
Ln{GM} Ln{μ} - 0.5*σl2 |
|
GSD μ, σ |
σl = σl = |
Ln{GSD} √{ Ln[1+σ2/μ2]} |
|
μl, σl |
Мода |
exp(μl - σl2) = самое часто встречающееся значение |
Ссылки
М-1. Leidel and KA Busch: Statistical Methods for the Determination of Non-compliance with Occupational Health Standards. NIOSH Technical Information, HEW Pub. No. 75-159, Cincinnati, Ohio.
М-2. Roach RA: Testing Compliance with ACGIH Threshold Limit Values for Respirable Dusts Evaluated by Count. Transactions of the American Industrial Hygiene Association, pp. 27-39, 1966.
М-3. Roach SA: A More Rational Basis for Air Sampling Programs. American Industrial Hygiene Association Journal 27:1-12, 1966.
М-4. Roach SA, EJ Baier, HE Ayer and RL Harris: Testing Compliance with Threshold Limit Values for Respirable Dusts. American Industrial Hygiene Association Journal 28:543-553, 1967.
М-5. Kerr GW: Use of Statistical Methodology in Environmental Monitoring. American Industrial Hygiene Association Journal 23:75-82, 1962.
М-6. Larsen RI: A Method for Determining Source Reduction Required to Meet Quality Standards. Journal of Air Pollution Control Association 11:71, 1961.
М-7. Larsen RI: A New Mathematical Model of Air Pollutant Concentration Averaging Time and Frequency. Journal of Air Pollution Control Association 19:24, 1969.
М-8. Phinney DE and JE Newman: The Precision Associated with the Sampling Frequencies of Total Particulate at Indianapolis, Indiana. Journal of the Air Pollution Control Association, 22:692-695, 1972.
М-9. Larsen RI: A Mathematical Model for Relating Air Quality Measurements to Air Quality Standards. US Environmental Protection Agency. AP-89, 1971.
М-10. Breslin AJ, Ong L, H Glauberman, AC Gejrge and P LeClare: The Accuracy of Dust Exposure Estimates Obtained from Conventional Air Sampling. American Industrial Hygiene Association Journal 28:56-61, 1967.
М-11. Sherwood RJ: On the Interpretation of Air Sampling for Radioactive Particles. American Industrial Hygiene Association Journal 27:98-109, 1966.
М-12. Sherwood RJ: The monitoring of Benzene Ehposure by Air Sampling. American Industrial Hygiene Association Journal 32:840-846, 1971.
М-13. Jones AR and Brief: Evaluating Benzene Exposures. American Industrial Hygiene Association Journal. 32:610-613, 1971.
М-14. Gale HJ: The Lognormal Distribution and Some Examples of Its Application in the Field of Radiation Protection. Atomic Energy Research Establishment Report AERE-R 4736, Her Majesty’s Stationery Office, London, England, 1965.
М-15. Gale HJ. Some Examples of the Application of the Lognormal Distribution in Radiation Protection. Annals of Occupational Hygiene, 10:39-45, 1967.
М-16. Coenen W: The Confidence Limits for the Mean Values of Dust Concentration. Staub (English Translation), 26:39-45, May 1966.
М-17. Coenen W: Measurement Assessment of the Concentration of Health Impairing, Especially Silicogenic Dusts at Work Places of Surface Industries. Staub (English Translation), 31:16-23, December 1971.
М-18. Hounam RF: An Application of the Log-Normal Distribution to Some Air Sampling Results and Recommendations on the Interpretation of Air Sampling Data. Atomic Energy Research Establishment Report AERE-M 1469. Her Majesty’s Stationery Office, London, England, 1965.
М-19. Juda J and K Budzinski: Feher bei der Bestimmiung der mittleren Staub-konzentration als Funktion der Anzahl der Einzelmessugen (Errors in Determinating the Mean Dust Concentration as a Function of the Number of Individual Measurements). Staub, 24:283-287 (English translation), Augest 1987.
M-20. Juda J and K Budzinski: Determining the Tolerance Range of the Mean Value of Dust Concentration, Staub, 27:12-16 (English translation), April 1987.
М-21. LeCare PL, AJ Breslin and L Ong: Factors Affecting the Accuracy of Average Dust Concentration Measurements. American Industrial Hygiene Association Journal 30:386-393, 1969.
М-22. Hald A: Statistical Theory with Engineering Applications. John Wiley and Sons, New York, NY 1952.
М-23. Aitchinson J and JAC Brown: The Lognormal Distribution. Cambridge University Press, Cambridge, England 1963.



Полезная информация: