Чрезвычайные ситуации → Эколого-экономическая деятельность предприятий → Прибыль производителя. Максимизация прибыли при чрезвычайных ситуацияхПерейдем непосредственно к подсчету прибыли производителя.
Обозначим:
Сп - затраты производителя на единицу продукции, Vn — прибыль производителя, Т - экологическая выплата. Тогда прибыль производителя есть
Руководствуясь процедурой осуществления экологических платежей и не рассматривая вариант выплаты штрафов за загрязнения (которые не входят явно в себестоимость товара), можно записать, что величина выплаты есть.
Что касается себестоимости продукции конкурента, рассматривать экологическую составляющую при нашей постановке задачи нет смысла, тем более что конкурент может быть всего лишь перепродавцом произведенной кем-то продукции.
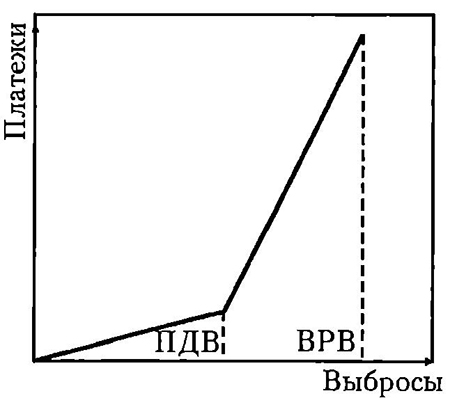
Рис.3.9. Зависимость платежей от выбросов
Теперь из формулы (3.1) выразим QK:
подставим в (3.8):
QnPn + QnPaPK =ф,
выразим Qn:
Qn = Ф / (Pп + Pарк)
Подстановкой в выражение (9а) получаем, что
Введем в рассмотрение новую переменную - издержки производства по отношению к стоимости товара конкурента.
Графически функция представлена на рис.3.10. Очевидно, что цена производителя должна быть выше себестоимости продукта и не превышать стоимость товара конкурента, то есть Сп < Рп < Рк, или с учетом введенных выше обозначений С<Р<1.
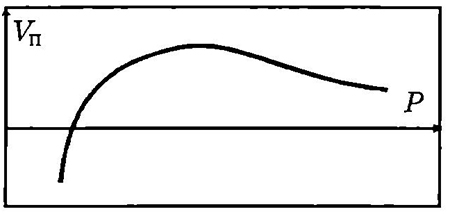
Рис.3.10. Зависимость прибыли от отношения цен
В ситуации, когда рыночные цены у производителя и импортера совпадают (Р =1), формула (3.12) приобретает вид:
то есть прибыль не зависит от эластичности а.
Как уже предполагалось выше, существует Рпопт, при котором товаропроизводитель получит максимум прибыли. Для нахождения экстремума продифференцируем функцию (3.12) по переменной Р и приравняем ее к нулю.
Из полученного уравнения нельзя в явном виде выразить переменную Р, поэтому для решения возникшей проблемы на практике необходимо привлекать численные методы поиска экстремума функции, например метод золотого сечения. В качестве отправного интервала разумно выбрать интервал [Сп,РК].