Как было сказано ранее, параметр а есть эластичность замещения спроса на товар производителя аналогичным товаром, представленным конкурентом. Понимая, что точно предугадать реакцию населения на потребительском рынке крайне сложно, имеет смысл рассматривать эластичность как случайную величину. Объективной характеристикой случайной величины является распределение случайной величины. Именно распределение и только его мы в принципе можем восстановить в реальном эксперименте. Будем считать, что эластичность равномерно распределена на интервале [а,b].
В качестве примечания необходимо заметить, что автором работы рассматривался случай распределения эластичности по закону Симпсона («треугольного» распределения), однако он не дал при решении практических задач сколь-нибудь существенных расхождений по сравнению с равномерным, лишь только усложнив расчеты и конечные формулы, приведя на промежуточном этапе к несчитаемым аналитически интегралам.
Договорившись оперировать с эластичностью а как со случайной величиной и вспоминая, что прибыль товаропроизводителя непосредственно зависит от нее, логично говорить о том, что прибыль также по природе своей случайна. Возникает, правда, вопрос: считать ли прибыль непрерывной или же дискретной случайной величиной?
Действительно, с одной стороны областью определения а является область действительных чисел, а область отображения функции вида также принадлежит R1. С другой стороны, прибыль выражается в денежном эквиваленте, т.е. будет величиной дискретной. Разрешим этот вопрос таким образом: везде далее считать прибыль непрерывной случайной величиной, и лишь на этапе практической реализации при выводе конечных числовых данных округлять их с определенной точностью.
Замечание: ранее было показано, что в случае равенства цен прибыль производителя не зависит от эластичности а. Поэтому нижеследующие рассуждения не затрагивают ситуацию равенства рыночных цен производителя и конкурента, то есть случая, когда Р = 1.
Известно, что одной из важнейших характеристик случайной величины является плотность распределения случайной величины. Зная плотность, можно определить, например, вероятность попадания величины в запрашиваемый интервал (что крайне полезно в нашей задаче), а также такую немаловажную числовую характеристику, как математическое ожидание. Перейдем к вычислению плотности распределения прибыли производителя.
В нашем случае стоит задача подсчета плотности распределения как функции от случайной величины а. Воспользуемся следующей теоремой:
Пусть Е, - непрерывная случайная величина с плотностью распределения рЕ(х). Пусть у = ф(Е) - монотонно-дифференцируемая функция. Тогда


Плотность ра(х) принимает ненулевые значения на интервале [а, b]. Выясним границы интервала [а, b], на котором плотность распределения у отлична от нуля.

Проанализируем выражение под знаком модуля. Так как уе [Vn(a), Vn(b)], то можно записать, что

График плотности распределения показан на рис.3.11.
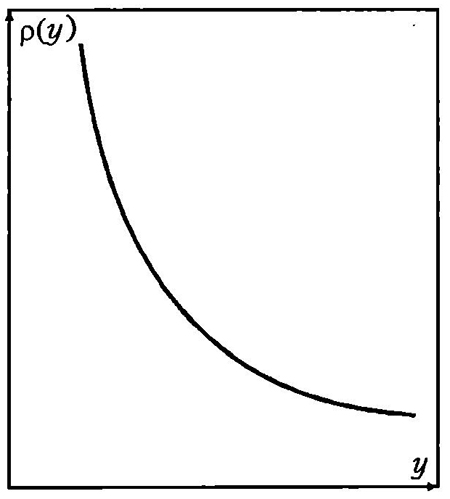
Рис.3.11. Плотность распределения прибыли товаропроизводителя
Перейдем к подсчету математического ожидания прибыли товаропроизводителя. Вспомним, что для непрерывной случайной величины

Учитывая, что Р > 0, от логарифма абсолютного значения выражения можно перейти к логарифму выражения. Запишем окончательно формулу для определения математического ожидания прибыли:
