Методы и модели оценки риска за последние 20 лет менялись, совершенствовались и, естественно, усложнялись в условиях неопределенности. Наиболее простые - статистические, вероятностные, а затем «деревья отказов» во многих работах получили широкое распространение. На смену им пришли методы «игры с природой». Последние представляют несколько экзотический характер, хотя при оценке экологического риска во многих работах используются. В последние годы развитие получили «экспертные методы» - наиболее перспективные и интенсивно совершенствующиеся. Это методы и модели типа ЧМС - «человеко-машины - системы».
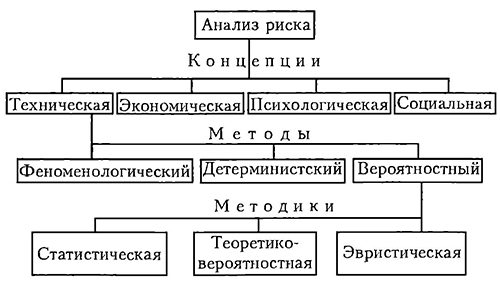
Рис.8.1. Методический аппарат анализа риска
Для оценки степени опасности важны не только частота (или вероятность) ее появления, но и тяжесть последствий для индивидуума, общества или окружающей среды.
Чтобы оценка была количественной, вводят понятие риска R, определяемого как произведение вероятности Р неблагоприятного события (аварии, катастрофы и т.д.) и ожидаемого ущерба У в результате этого события:

если могут иметь место несколько (г) неблагоприятных событий с различными вероятностями и соответствующими им ущербами. Выражение для риска может быть записано в виде интеграла:
где F(Y) — весовая функция потерь, с помощью которой последствия различной природы приводятся к единой (например, стоимостной) оценке ущерба; р(Y) - плотность распределения случайной величины Y (в общем случае векторной).
В такой формулировке риск - мера опасности, определяется как математическое ожидание ущерба или потерь. Так, в методиках оценки комплексного риска для населения от чрезвычайных ситуаций природного и техногенного характера риск, как математическое ожидание потерь людей M[N] в пределах некоторой территории (например, города), определяется по формуле:

где Р — вероятность аварии или чрезвычайной ситуации (ЧС), в результате которой возникает поражающий фактор, характеризуемый параметром Ф (например, интенсивность землетрясения, избыточное давление на фронте ударной волны, токсодоза и т.д.); Фmin, Фmах — соответственно минимально и максимально возможное значение параметра поражающего фактора; Р(Ф) — вероятность поражения людей в зависимости от Ф как параметра (часто задается в виде функции нормального распределения от пробит-функции параметра Ф); f(х, у) — плотность населения в пределах рассматриваемой площадки; f(х,у,Ф) — плотность распределения интенсивности параметра Ф в пределах площадки с координатами (х,у).
В общем случае при учете фактора времени риск является функционалом, зависящим от реализации случайного процесса, описывающего течение или сценарий неблагоприятного события.
В табл.8.3 приведены некоторые уравнения для вычисления риска при выбросе вредных веществ.
Таблица 8.3. Уравнения для вычисления некоторых показателей риска при авариях, связанных с выбросами вредных веществ

Здесь: Р(А)i — вероятность аварии по сценарию I; Рij(ху) — вероятность реализации механизма воздействия j в точке (х, у) для сценария выброса г; P(L)j — вероятность летального исхода (или заболевания) при реализации механизма воздействия j; N(x,y) — численность людей в ячейке (единичной площадке) с координатами (х,у); Рi — вероятность негативных последствий при реализации аварийного сценария i; Ni — число смертельных исходов при реализации аварийного сценария i.
Большинство методов, используемых при анализе рисков, позволяют решать вероятностные проблемы, сводя их к задачам теории вероятностей и математического анализа, решение которых, в свою очередь, можно получить аналитически или численно.
Метод Монте-Карло, называемый также методом статистического моделирования, позволяет решать вероятностные проблемы статистическими средствами. Электронные вычислительные машины позволяют легко получать так называемые псевдослучайные числа, которые при решении задач используются как случайные. С появлением современной вычислительной техники метод Монте-Карло находит все более широкое применение в различных областях науки и техники для исследования различного рода систем (автоматического управления, экономических, биологических, технических и т.д.) практически любой сложности. Важная особенность метода — его простота, о чем свидетельствует рассмотрение ряда работ.
Так, в работе предлагается использовать метод статистического моделирования для оценки и анализа техногенного риска. Подход основан на моделировании поведения сложных систем, когда аналитическое решение затруднено или невозможно. В подходе используются функции воздействия на систему и соответствующие функции проявления негативных для системы эффектов. Это позволяет более адекватно оценить риск, поскольку результатом моделирования является дифференциальное распределение риска на всю совокупность объектов воздействия. Параметры этого распределения могут служить основой для детального анализа, верификации принятой модели риска и принятия решений в конкретных практических ситуациях или при прогнозировании катастроф.
Обычный статистический метод прогнозирования, основанный на последовательности предположение - проверка - моделирование - прогноз, не может быть успешно использован к описанию нелинейных природных процессов. Предлагаемая регрессионная модель в качестве первой ступени последовательности рассматривает процедуру оценки имеющихся данных (и пополнение БД в случае се недостаточного объема). Это позволяет в определенной мере решить проблему нелинейности и аномальности природных процессов. В работе модель рассматривается на примере загрязнения атмосферы SO2; точность соответствия достигает 96%, а точность прогнозирования -80%, что намного выше аналогичных характеристик в прогнозировании с использованием моделей с неопределенными критериями.
Среди методов оценки деятельности производственных систем при анализе риска достаточно активно используется метод построения «дерева отказов». Он является некоторой иллюстрацией вероятностных методов и представляет значительный интерес для специалистов, связанных с эксплуатацией, обслуживанием и надзором технических объектов. Имея такую схему, специалист, даже не обладая основательными знаниями по теории вероятностей, может не только найти наиболее критический вариант развития событий, по и оценить ожидаемый риск, если соответствующее дерево событий или отказов дополнено статистическими данными. Кроме того, па рынке коммерческих специализированных программ уже давно имеются программные комплексы для автоматизированного построения деревьев отказов и деревьев событий сложных систем.
Дерево отказов (дерево аварий) представляет собой сложную графологическую структуру, лежащую в основе словесно- графического способа анализа возникновения аварии из последовательностей и комбинаций, и неисправностей, и отказов элементов системы.