Техническое приложение В
Непостоянство воздействия в производственных группах, у которых ожидается схожий риск воздействия
В прошлом для определения воздействия на группу рабочих со схожим уровням риска в промышленной гигиене было принято проводить измерения лишь у небольшой группы рабочих. Измеренные воздействия усредняли, и это усреднённое воздействие на небольшую подгруппу рабочих считали соответствующим воздействию на всю группу рабочих.
Такой компромиссный способ проведения измерений объяснялся небольшим числом промышленных гигиенистов и ограниченными, небольшими возможностями для измерений воздействия на каждого из рабочих. Кроме того считалось, что в группе рабочих изменчивость средних воздействий небольшая, и что между средним значением и наибольшим и наименьшим воздействиями различие невелико.
Работа (В-1) внесла большой вклад в промышленную гигиену, так как показала, что описанная выше процедура (измерения воздействия) вносит неточность. В статье обсуждается отличие между максимальным среднесменным воздействием на отдельного рабочего, и средним значением среднесменного воздействия у группы рабочих. К сожалению, на эту статью не обратили внимания.
Их работа имеет большое значение, так как Закон об охране труда от 1970г требует [ раздел 6(b)7 ], чтобы Минтруда (США) разрабатывал стандарты по охране труда, которые '' … должны обеспечить наблюдение и измерение воздействий на сотрудников в таких местах и с такими интервалами, и такими способами, которые могут потребоваться для защиты (жизни и здоровья) сотрудников.''
В (В-1) обнаружили, что распределение значений воздействия соответствует, в основном, логарифмически-нормальному закону распределения. Это распределение, и его использование при измерении производственных воздействий обсуждаются в (В-3) и (В-4). То, что в группе рабочих средние значения воздействий соответствуют логарифмически-нормальному распределению, приводит к важным последствиям.
У группы рабочих, у которых (имеется) стандартное геометрическое отклонение средних воздействий GSD, значения средних воздействий на отдельных рабочих очень разнообразны, и могут отличаться на порядок. Отношение воздействия на 95%-го рабочего (такого рабочего, у которого среднее воздействие превышает 95% от средних воздействий на всех рабочих в группе) к среднему арифметическому воздействию в этой группе обычно составляет 2:1 ÷ 3:1. То есть, воздействие на 95%-го рабочего может составлять от 200 до 300% от среднего воздействия в группе.
На Фиг. В-1 графически показано распределение воздействий на рабочих в группе для разных значений параметров воздействия. Истинное среднее арифметическое воздействие μ со (средним геометрическим GM и стандартным геометрическим отклонением GSD) :
μ = GM * exp [0.5 (Ln GSD)2 ], где
μ - истинное среднее арифметическое воздействие в группе.
GM – истинное среднее геометрическое воздействие в группе (= воздействию на 50%-го рабочего)
GSD – истинное стандартное геометрическое отклонение для распределения воздействий в группе.
Эта формула использовалась для построения Фиг. В-1 и вычисления значений в таблице В-1. Во всех случаях, истинное среднее арифметическое значение в группе было постоянным - 100 ppm.
В (В-1) и (В-4) представлены таблицы, которые показывают, что значения GSD в группе рабочих обычно находятся в диапазоне от 1.5 до 2.5. Таблица В-1 показывает, что если считать, что у всех рабочих в группе воздействие равно среднему арифметическому, то воздействие у не менее 5% рабочих составит от 56 до 34% от реального воздействия на них (при GSD от 1.5 до 2.5)..
В такой ситуации некорректно считать, что воздействие на отдельных рабочих равно/схоже со средним воздействием на группу из всех сотрудников, так как среднее значение для всей группы значительно ниже максимальных значений воздействия на отдельных рабочих. Только при маленьких GSD у группы (~1.15, или меньше) можно считать, что воздействие на отдельных сотрудников соответствует среднему арифметическому воздействия на группу (с погрешностью меньше 20%). Но для определения GSD нужно сделать много измерений, и в подавляющем большинстве случаев GSD будет больше 1.15.
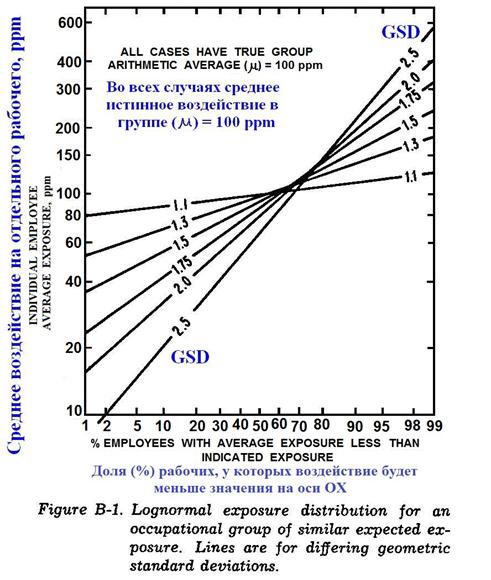
Фиг. В-1. Логарифмически-нормальное распределение производственного воздействия у группы рабочих со схожим ожидаемым воздействием. Разным прямым соответствуют разные GSD
Таблица В-1. Наибольшие воздействия при логарифмически-нормальном распределении
GSD
GM, ppm
90%-е воздействие, ppm
95%-е воздействие, ppm
Отношение 95%-го воздействия к среднему в группе
Среднее воздействие в группе как доля (%) от 95%-го воздействия
1.1
99.5
112
116
1.16
86%
1.3
97
135
149
1.49
67%
1.5
92
155
179
1.79
56%
1.75
86
175
215
2.15
47%
2.0
79
191
246
2.46
41%
2.5
66
213
297
2.97
34%
Ссылки
В-1. Ayer H.E. and J. Burg: Time-Weighted Average vs. Maximum Personal Sample. Paper presented at the 1973 American Industrial Hygiene Conference in Boston, Mas.
В-2. Public Law 91-596, 91st Congress, December 29, 1970.
В-3. Leidel NA and Busch KA: Statistical Methods for the Determination of Non-compliance with Occupational Health Standards. NIOSH Technical Information, HEW Pub. No. (NIOSH) 75-159, Cincinnati, Ohio 45226, April 1975.
В-4. Leidel NA, KA Busch and WE Crouse: Exposure Measurement Action Level and Occupational Environmental Variability. NIOSH Technical Information, HEW Pub. No. (NIOSH) 76-131, Cincinnati, Ohio 45226, December 1975.



Полезная информация:
Непостоянство воздействия в производственных группах, у которых ожидается схожий риск воздействия
В прошлом для определения воздействия на группу рабочих со схожим уровням риска в промышленной гигиене было принято проводить измерения лишь у небольшой группы рабочих. Измеренные воздействия усредняли, и это усреднённое воздействие на небольшую подгруппу рабочих считали соответствующим воздействию на всю группу рабочих.
Такой компромиссный способ проведения измерений объяснялся небольшим числом промышленных гигиенистов и ограниченными, небольшими возможностями для измерений воздействия на каждого из рабочих. Кроме того считалось, что в группе рабочих изменчивость средних воздействий небольшая, и что между средним значением и наибольшим и наименьшим воздействиями различие невелико.
Работа (В-1) внесла большой вклад в промышленную гигиену, так как показала, что описанная выше процедура (измерения воздействия) вносит неточность. В статье обсуждается отличие между максимальным среднесменным воздействием на отдельного рабочего, и средним значением среднесменного воздействия у группы рабочих. К сожалению, на эту статью не обратили внимания.
Их работа имеет большое значение, так как Закон об охране труда от 1970г требует [ раздел 6(b)7 ], чтобы Минтруда (США) разрабатывал стандарты по охране труда, которые '' … должны обеспечить наблюдение и измерение воздействий на сотрудников в таких местах и с такими интервалами, и такими способами, которые могут потребоваться для защиты (жизни и здоровья) сотрудников.''
В (В-1) обнаружили, что распределение значений воздействия соответствует, в основном, логарифмически-нормальному закону распределения. Это распределение, и его использование при измерении производственных воздействий обсуждаются в (В-3) и (В-4). То, что в группе рабочих средние значения воздействий соответствуют логарифмически-нормальному распределению, приводит к важным последствиям.
У группы рабочих, у которых (имеется) стандартное геометрическое отклонение средних воздействий GSD, значения средних воздействий на отдельных рабочих очень разнообразны, и могут отличаться на порядок. Отношение воздействия на 95%-го рабочего (такого рабочего, у которого среднее воздействие превышает 95% от средних воздействий на всех рабочих в группе) к среднему арифметическому воздействию в этой группе обычно составляет 2:1 ÷ 3:1. То есть, воздействие на 95%-го рабочего может составлять от 200 до 300% от среднего воздействия в группе.
На Фиг. В-1 графически показано распределение воздействий на рабочих в группе для разных значений параметров воздействия. Истинное среднее арифметическое воздействие μ со (средним геометрическим GM и стандартным геометрическим отклонением GSD) :
μ = GM * exp [0.5 (Ln GSD)2 ], где
μ - истинное среднее арифметическое воздействие в группе.
GM – истинное среднее геометрическое воздействие в группе (= воздействию на 50%-го рабочего)
GSD – истинное стандартное геометрическое отклонение для распределения воздействий в группе.
Эта формула использовалась для построения Фиг. В-1 и вычисления значений в таблице В-1. Во всех случаях, истинное среднее арифметическое значение в группе было постоянным - 100 ppm.
В (В-1) и (В-4) представлены таблицы, которые показывают, что значения GSD в группе рабочих обычно находятся в диапазоне от 1.5 до 2.5. Таблица В-1 показывает, что если считать, что у всех рабочих в группе воздействие равно среднему арифметическому, то воздействие у не менее 5% рабочих составит от 56 до 34% от реального воздействия на них (при GSD от 1.5 до 2.5)..
В такой ситуации некорректно считать, что воздействие на отдельных рабочих равно/схоже со средним воздействием на группу из всех сотрудников, так как среднее значение для всей группы значительно ниже максимальных значений воздействия на отдельных рабочих. Только при маленьких GSD у группы (~1.15, или меньше) можно считать, что воздействие на отдельных сотрудников соответствует среднему арифметическому воздействия на группу (с погрешностью меньше 20%). Но для определения GSD нужно сделать много измерений, и в подавляющем большинстве случаев GSD будет больше 1.15.

Фиг. В-1. Логарифмически-нормальное распределение производственного воздействия у группы рабочих со схожим ожидаемым воздействием. Разным прямым соответствуют разные GSD
Таблица В-1. Наибольшие воздействия при логарифмически-нормальном распределении
|
GSD |
GM, ppm |
90%-е воздействие, ppm |
95%-е воздействие, ppm |
Отношение 95%-го воздействия к среднему в группе |
Среднее воздействие в группе как доля (%) от 95%-го воздействия |
|
1.1 |
99.5 |
112 |
116 |
1.16 |
86% |
|
1.3 |
97 |
135 |
149 |
1.49 |
67% |
|
1.5 |
92 |
155 |
179 |
1.79 |
56% |
|
1.75 |
86 |
175 |
215 |
2.15 |
47% |
|
2.0 |
79 |
191 |
246 |
2.46 |
41% |
|
2.5 |
66 |
213 |
297 |
2.97 |
34% |
Ссылки
В-1. Ayer H.E. and J. Burg: Time-Weighted Average vs. Maximum Personal Sample. Paper presented at the 1973 American Industrial Hygiene Conference in Boston, Mas.
В-2. Public Law 91-596, 91st Congress, December 29, 1970.
В-3. Leidel NA and Busch KA: Statistical Methods for the Determination of Non-compliance with Occupational Health Standards. NIOSH Technical Information, HEW Pub. No. (NIOSH) 75-159, Cincinnati, Ohio 45226, April 1975.
В-4. Leidel NA, KA Busch and WE Crouse: Exposure Measurement Action Level and Occupational Environmental Variability. NIOSH Technical Information, HEW Pub. No. (NIOSH) 76-131, Cincinnati, Ohio 45226, December 1975.



Полезная информация: